正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の 四角錐台の体積の求め方 中学一年の者です。とても急いでいるので質問が乱暴になってしまってすいません。 どなたか、四角錐台(四角錐の上部を切り取ったようなもの)の体積の求め方を教えてください!! お願いします。 ベストアンサー 数学・算数;直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積

計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
正方形の体積の求め方
正方形の体積の求め方-このことを用いると,上の図1において, 正方形の面積は,2×2=4(cm2)で, 重心(対角線の交点)がえがく円周の長さは,2π×1=2π(cm)なので, この正方形を回転させてできる立体の体積は, 4×2π=8π(cm3)と求めることができます。(円柱の体積)=(半径rの円の面積)×(半径rの球の高さ) だから、 =( × × π )×( × ) = ×




体積の求め方 計算公式一覧
基本的には今まで説明した四角柱の体積と表面積の求めた方と同じですが、正六面体について説明します。 こちらはおまけ程度に確認してください。 立方体の体積 例えば、一辺が2cmの立方体の体積について考えてみましょう。 立方体(正六面体)という図形が持つ特殊性を全く考えな (正方形abcd) = (対角線ac)×(対角線bd)÷2 = 10×10÷2 = 50 cm^2 になるよ。 計算ミスしないように、ゆっくり解いてみてね!なので、 二等辺三角形の面積を求めて、それを8つ分にする。 という考え方で正八角形の面積を求めていきます。 中心の360°を8等分していることから 二等辺三角形の頂角は であることが分かりますね。 そして、次のように補助線を引くと 45°、45°、90°の直角三角形が作れます。 よって、二等辺三角形の高さにあたる辺の長さを求めることができます。 よって
正方形の面積 A: 面積: 長方形の面積 A: B: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形(例1)正四角錐OABCDが あります。底面ABCDは、 1辺の長さが6cmの正方 形で、ほかの辺の長さはすべ小学5年生の算数立体の体積の求め方練習プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題
たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ! めんどい計算式だけど、 落ち着いて計算してみよう!「円の面積の求め方 1辺が10cmの正方形 2つ分より大きいことをとらえさせます。 外側の正方形の面積はどうかな? 半径10cmの円の外側に、正方形をかいて 円の面積のおよその大きさを考えよう 半径10cmの円の外側に正方形を書くと → 上の図のように、円の面積は、1辺10cmの正方形4つ分の面積ただし、高さの平均が使えるのは、底面が円、三角形、正 方形、長方形、ひし形、平行四辺形、正偶数角形のときだ け。 1 3 体積を求める問題のポイント 立体切断⑶ 体積 2 ステップ1 高さ平均 1 図のような1辺が12㎝の立方体があり、点Qは辺のまん中の点です。 いま、この立方体を3点P、Q、R
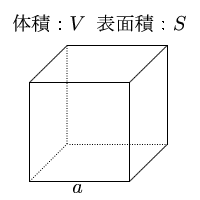



立方体の体積から1辺 体積 表面積の計算 計算サイト




マスラボ 小学校5年 体積 レベル3 立方体の体積の求め方 Youtube
長方形はごろりとねかすとたてと橫が変わるから、橫×たてで計算してもいいですよ。 計算は、こんなふうにやります。 ・1辺の長さが5cmの正方形の面積は、5×5=で、25cm 2 。 たて3cm、橫8cmの長方形の面積は、3×8=24、あるいはで8×3=24で24cm 2 。 以上、終わり。 かんたんでしょ。 どこででも練習できるごく面積の基本のパターンですね。 ページの先頭へ正四角錐の高さの求め方について底面が18cm四方の正方形側面の二等辺三 台形の体積 って何 相似の考え方を利用して四角錐台の体積を求め 錐体の表面積6 宿題解説 正四角錐の体積 表面積の求め方 Youtube 四角錐台 体積 中3 数学右の図3は正四角錐の投影図ですこの四角錐の 立面図は1これが四 コレクション 正方形 体積 2772正方形 体積の求め方 リンクを取得 ;




体積 容積の求め方 算数 教科質問ひろば 進研ゼミ小学講座
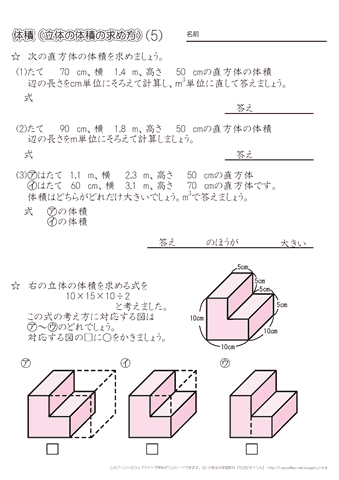



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
5月 14, 21 1・2年の復習lv3_3 6③解説 6③ 1辺18cmの正方形abcdでabの中点をe, aの中点をfとする。 ef,ec,fcを折り目として折り曲げて三角錐をつくる。この正四角錐の体積をVcm3とすると、 底動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru7章 三平方の定理 198 3 右の図のように,正方形 abcd の紙を,辺 ad の中点mと頂点c を結ぶ直線を折り目として折り返し,頂点dが移る点をe,線分 me の延長と辺 ab の交点をfとする。次の問いに答えよ。 ⑴ fe=fb であることを証明せよ。 ⑵ ad=2,fe=a とするとき,a の値を求めよ。また, afm の




小学校5年 算数 大きな体積とかさ 台の形の体積 Youtube




直方体と立方体の体積 算数 数学が好きになりmath
数学切り抜き帳 1辺の長さがaの正四面体の体積はいくらか. この問題は,真っ正直に考えればわかる問題である. じつは,そんなにかた苦しく考えなくても,簡単に答を求める方法がある. 簡単な方法というのは, 「立方体の中に,正四面体が隠れて全体の体積から 点線で囲んでいる小さな体積を引くと,7-80=640となり,この体積が 求められます。 1mは100cmなので,1m3 立方体,直方体の体積は,辺の長さが小数であっても計算 をして,求めることができます。 15cm 4cm C 10cm 12cm 8cm 14m 06m 07m A B三平方の定理を応用すると、正三角形の高さを求めることができる。 例題 右の図のような正三角形の高さ h を求めよ。 (解法) 正三角形 abc の頂点aから底辺bcに垂線ahをおろすと、図のように、点hはbcの中点になる。 なので、まずbhの長さは 1cm である。
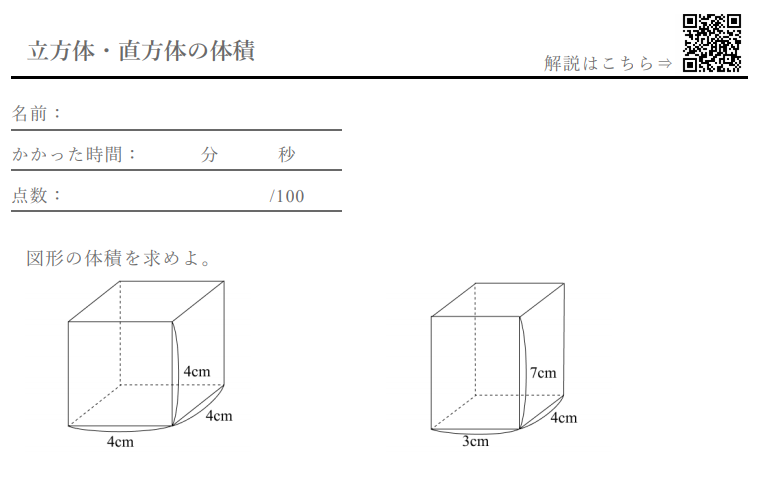



立方体 直方体 の体積 計算ドリル 問題集 数学fun




体積の求め方 計算公式一覧
・誘導起電力の向きの求め方 ①レンツの法則 誘導起電力は、回路をつらぬく磁束の変化を妨げる向きに起こる ②導体棒中の正電荷のキャリアが受けるローレンツ力の向きに誘導起電力は起こる で、掃過面積 要は、 磁束密度bに、導体が単位時間に磁場を垂直に横切る面積をかけるだけ正四面体の6つの辺の長さは等しく、これを a とします。正四面体の体積は、次の式で求まります。 正四面体 (せいしめんたい) の体積 \begin{align*} V = \frac{\sqrt{2}}{12}a^3 \end{align*} 体積 = 141 × 一辺 × 一辺 × 一辺 ÷ 12四角形 4角形 面積計算 公式 求め方 正方形 長方形 縦 横 自動 area 面積 四角形 面積;




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




この体積の求め方を教えてください Clear
体積の求め方プリントを 作ろう 直方体を描く 描画パレットの 基本図形をクリックし、 基本図形ツールボックスの 直方体3 をクリックします。 1 高さや奥行きを自由に設定して、直方体を描いてみましょう。 花子なら、直方体に寸法線を追加するのも簡単。描いた長さを 自動的に表示さ② 正方形(ひし形)の面積=対角線×対角線× 底面の正方形の対角線は6cmより, 2 6×6×12=18cm2 ③錐体の体積=底面積×高さ×3 ① ②より,この正四角錐の体積は, 18×33 ×13=1 cm3となります。一般的な求め方は, 1 4 のおうぎ形から三角形を引くと木の葉形の 1 2 の弓形 の面積が求められるのでこれを2倍します。 (10 10 314 1 4 10 10 2) 2 = (785 50) 2 = 285 2 = 57 µ 2円と正方形 右の図で,円の面積は正方形の面積の157倍です。 例題 (1) 右の図1 の斜線部分の面積を求めなさい。ただ



1
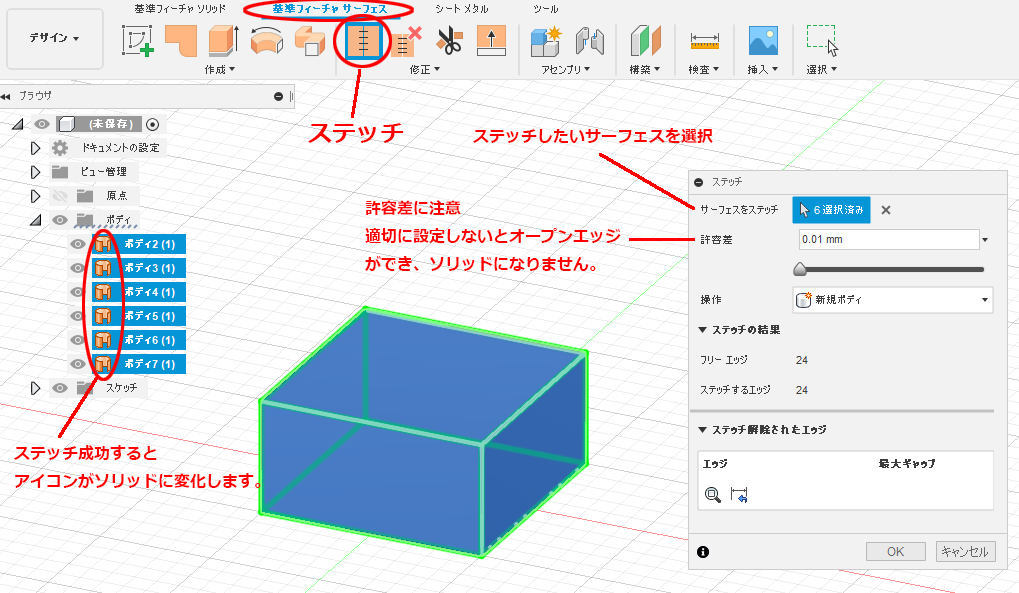



解決済み 面積 体積の求め方 Autodesk Community International Forums
図形の面積(体積)や周りの長さを文字式にする問題まとめ|中1数学(文字式) 1辺の長さが a cm の正方形 面積 : a 2 cm 2 周囲 : 4a cm 縦が a cm、横が b cm の長方形 面積 : ab cm 2 周囲 : 2 (ab) cm 底辺が a cm、高さが b cm の三角形 面積 : 1/2ab cm 2一辺の長さ $a$ の 正方形 (せいほうけい) の面積 $S$ は、次の公式で求められます。 正方形 (せいほうけい) の面積 \begin{align*} S = a^2 \end{align*} 面積 = 一辺 × 一辺三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。 体積を求めるには底面積×高さ÷3の公式を使いますが,そのためには高さOHを




直方体 立方体の体積 Youtube




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
求め方と公式 ・複合図形の体積 ・容積、内のりの意味 12)四角形と三角形の面積 ・公式を用いて,長方形や正方形 の面積を求めたり,辺の長さを 求めたりする。 ・周りの長さが等しい長方形や正 方形の面積を調べ,周りの長さ が等しくても面積が異なる図 形があることをおさえる。 技 この定義に従うと、正方形 ひし形の面積の求め方は、簡単なようで忘れがちです。 問題自体は簡単なものばかりなので、必ず公式を覚えておくようにしましょう! 補足 なお、「ひし形の作図方法」については以下の記事で説明しています。 四角形(ひし形・平行四辺形・台形)の書き方四角錐の体積の求め方 公式 小学生 中学生の勉強 正方形 四 角錐 の 体積 正方形 四 角錐 の 体積



算数流体積の求め方 Sciencelab 冨田塾
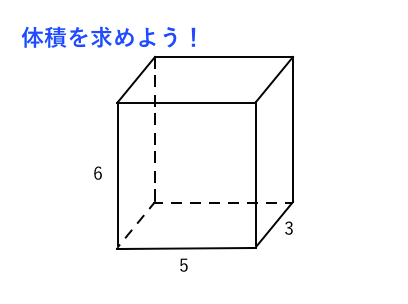



超簡単 体積の求め方 苦手な数学を簡単に
で求められます。 たとえば、「底辺 \(8cm\) 斜辺 \(10cm\) の三角形」の面積は \(\dfrac{1}{2}×8×\sqrt{10^28^2}=24cm^2\) 「1辺の長さ \(4cm\) の正三角形」の面積は \(\dfrac{\sqrt{3}}{4}×4^2=4\sqrt{3}cm^2\) となります。要点四角柱,三角柱,円柱の体積 四角柱,三角柱,円柱の体積 V は,底面積 S と高さ h を使って表すことができます. V=Sh 特に,円柱については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから V=πr 2 h と書くこともできます.角柱の体積の求め方を理解する ことができる。 ・四角柱の体積の求め方を基 に,三角柱の体積の求め方 を考えさせる。 ・四角柱の半分として求めた 体積と,底面積×高さで求 めた体積を比較し,同じで あることを確認させる。 ・他の図形(三角柱




長方形の面積の求め方 簡単な計算問題で公式を覚えよう 中学や高校の数学の計算問題




立体の体積を求める公式
今回は、体積の公式の求め方、覚え方と一覧、三角柱、円柱、三角錐の体積について説明します。体積の意味など下記も参考になります。 体積と重量の違いは?1分でわかる重量の計算、比重との違い、鉄の重量換算 容積とは?1分でわかる意味、求め方、単位、円柱の容積、体積との違い 100長方形、正方形断面 ⇒ 喫水=浮心×2 三角形(凸部分が水中に向く場合) ⇒ 喫水=浮心×3 ちなみに凸部分が上向きの場合、台形の重心位置が分かれば喫水が算定できます。




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com
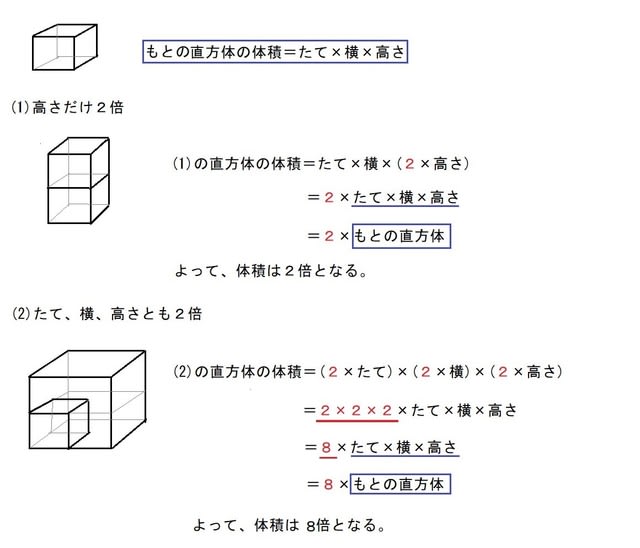



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support
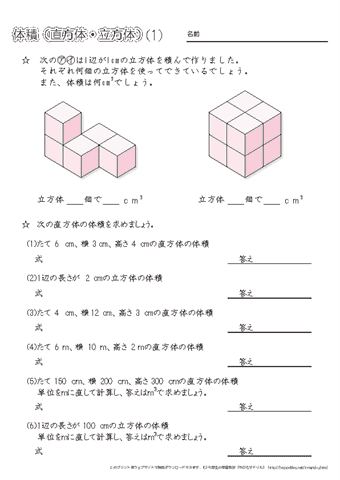



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生
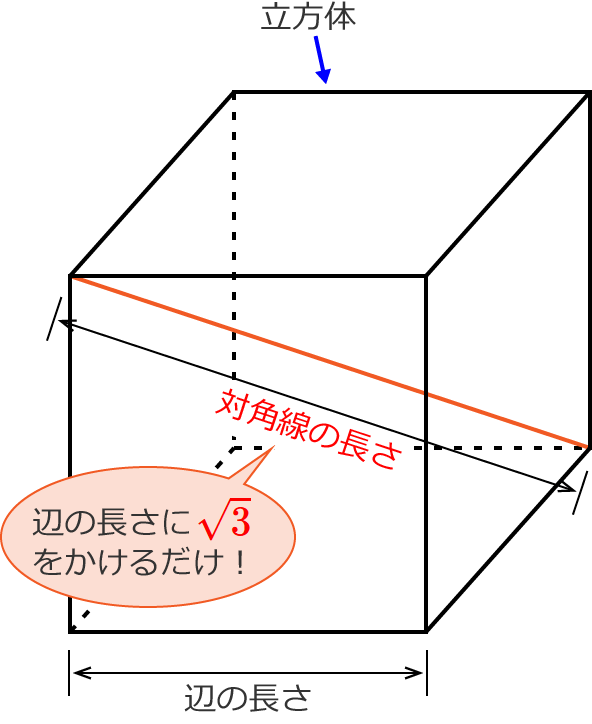



立方体の対角線の長さの求め方



Www Nagoya C Ed Jp School Shimizu E 5sansu A Pdf



6年算数立体の体積1 教え方




体積 表面積




体積の求め方 計算公式一覧
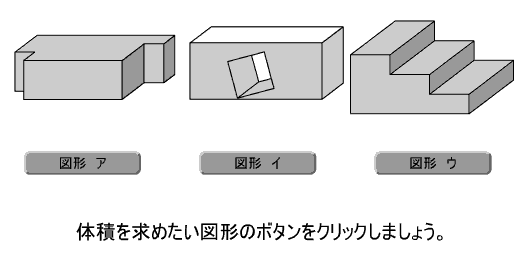



算数科5年 体積 導入 発展教材ソフトを使った授業 Note Board



Http Shima E Saitama City Ed Jp Kyukougadai 5nenn P19 5e23kotae Pdf




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



兵庫県実践事例 算数小学校6年
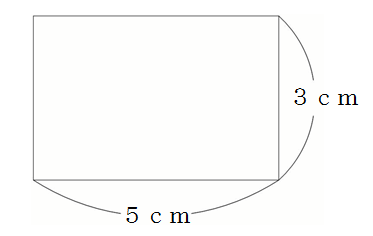



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント



穴のあいた立体の表面積 浦和明の星女子中学 2012年 どう解く 中学受験算数
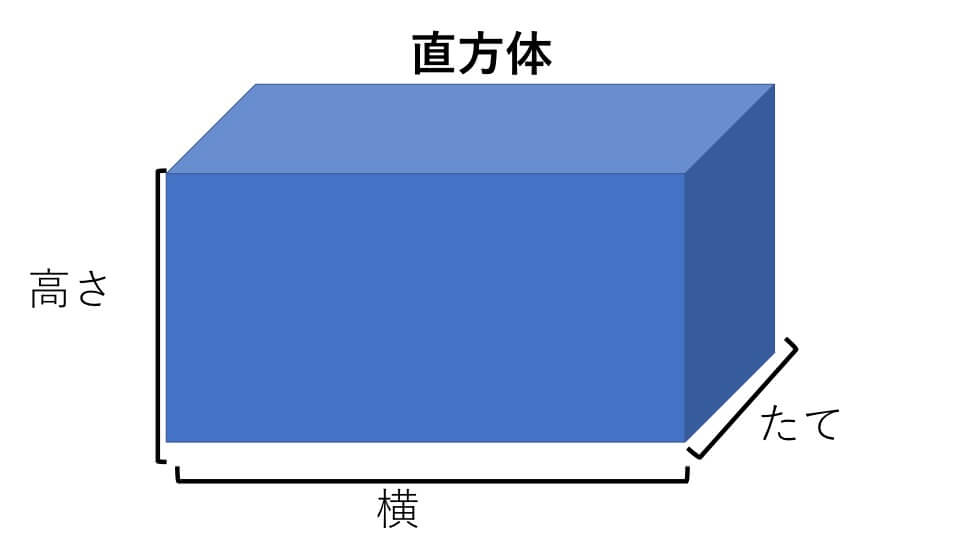



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 数学ノート




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書
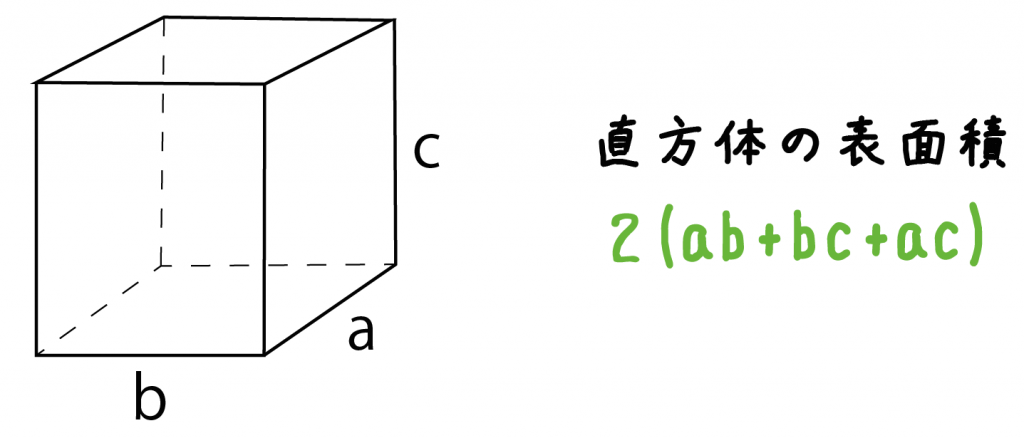



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




無料印刷可能 体積 容積 求め 方



1



1




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




小5 算数 小5 3 直方体と立方体の体積 Youtube




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
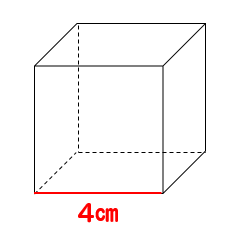



立方体の体積 小学生はどうやって問題解く 計算のやり方を解説 数スタ




体積の求め方 計算公式一覧
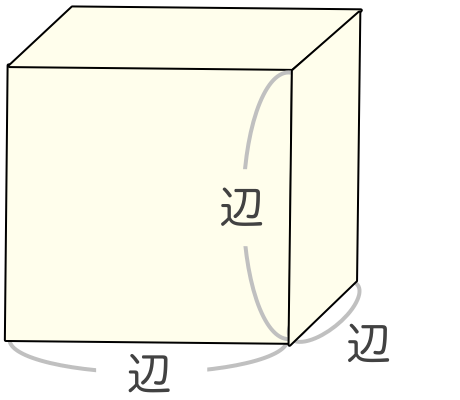



立方体の体積 簡単に計算できる電卓サイト
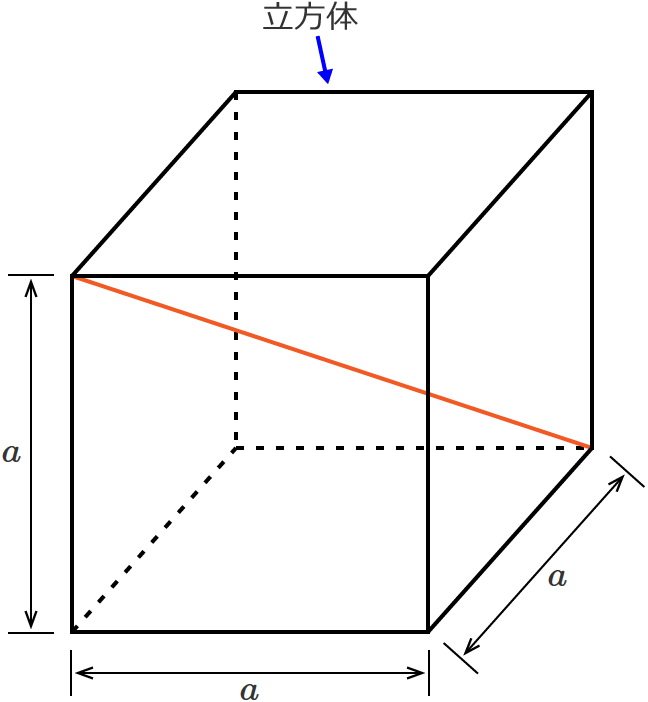



立方体の対角線の長さの求め方



5年算数体積2わかる教え方




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



Search Results For Page 312 横山験也のちょっと一休み




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
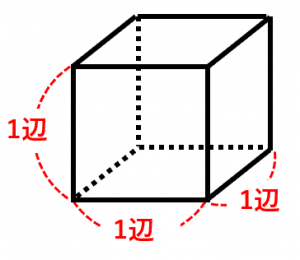



立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学



正方形 の 面積 の 求め 方 正方形の面積は 1分でわかる公式 対角線 ルートの関係 面積から辺の長さを求める方法 Amp Petmd Com




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
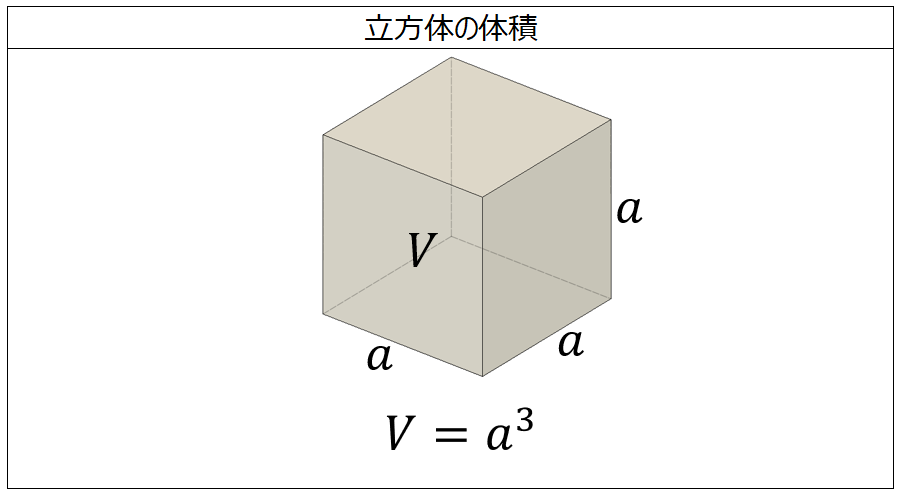



体積の計算 立方体 製品設計知識
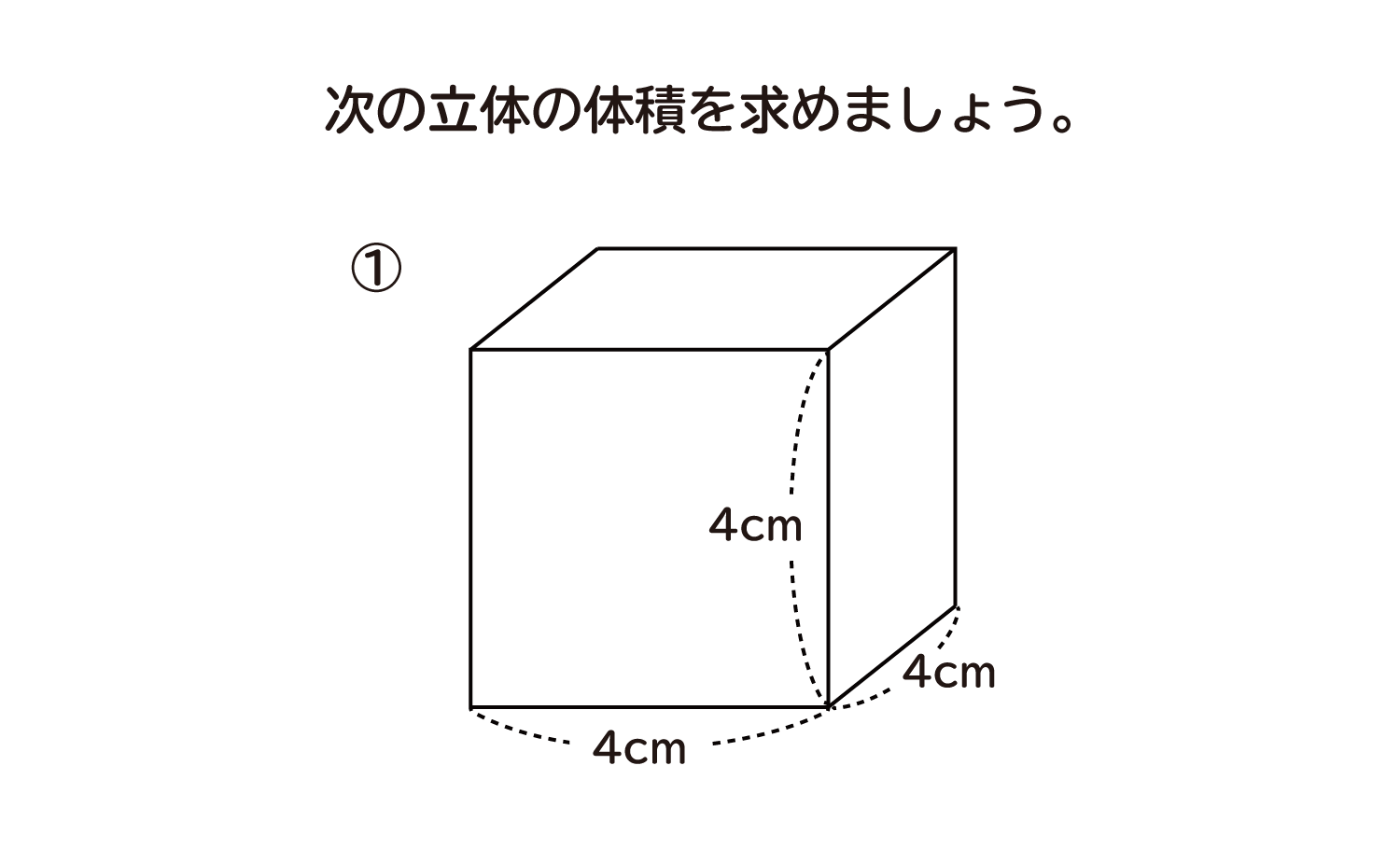



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



Studydoctor柱体や角錐の表面積の求め方 中学1年数学 Studydoctor
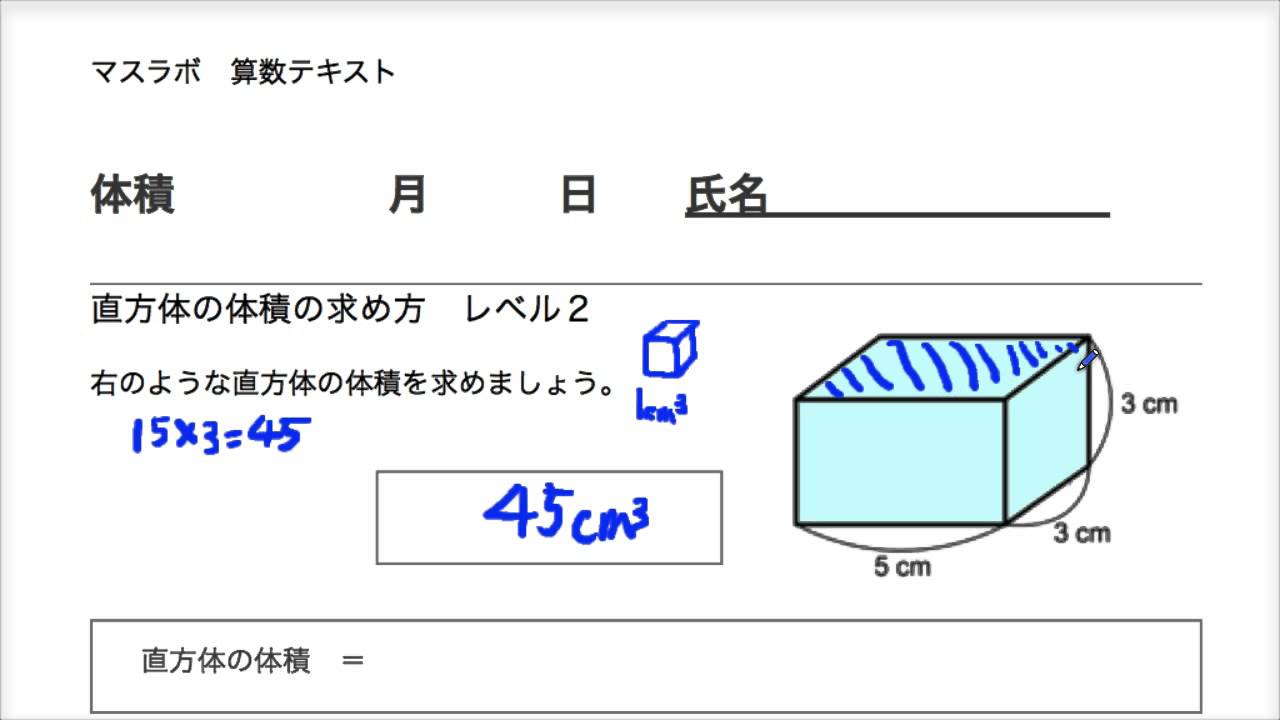



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




どうして1 3なの 錐の体積の公式の求め方 まなべーと



5年算数体積2わかる教え方




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト
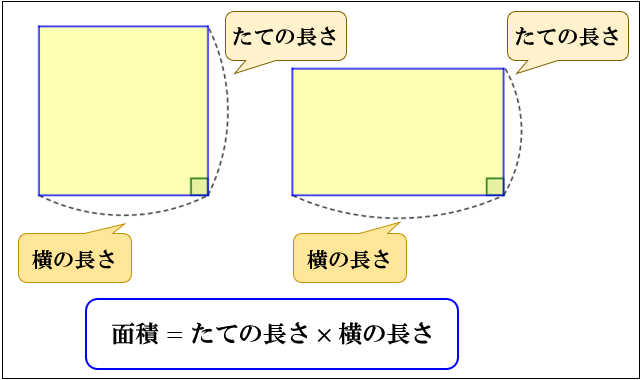



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




四角錐台の体積 高精度計算サイト
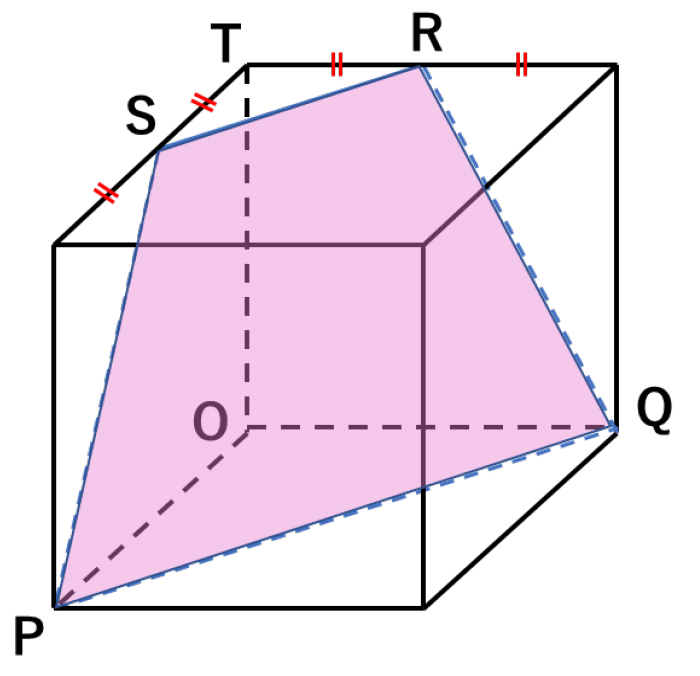



よく見かけますね この展開図 後編 中学受験プロ講師ブログ
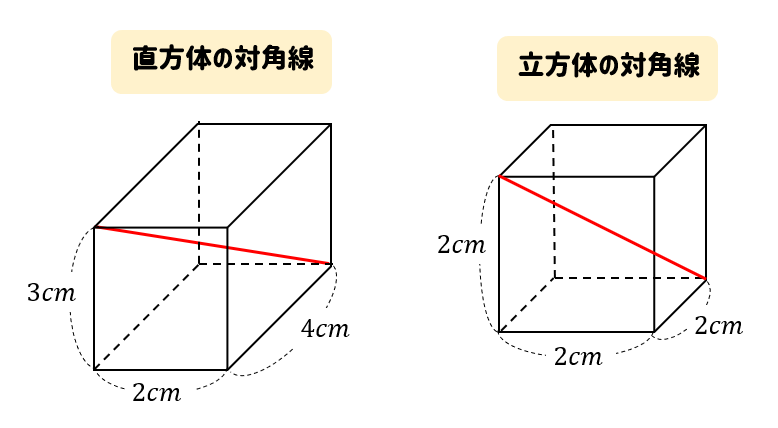



直方体 立方体の対角線の長さは公式でラクラク計算できるぞ 数スタ




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生
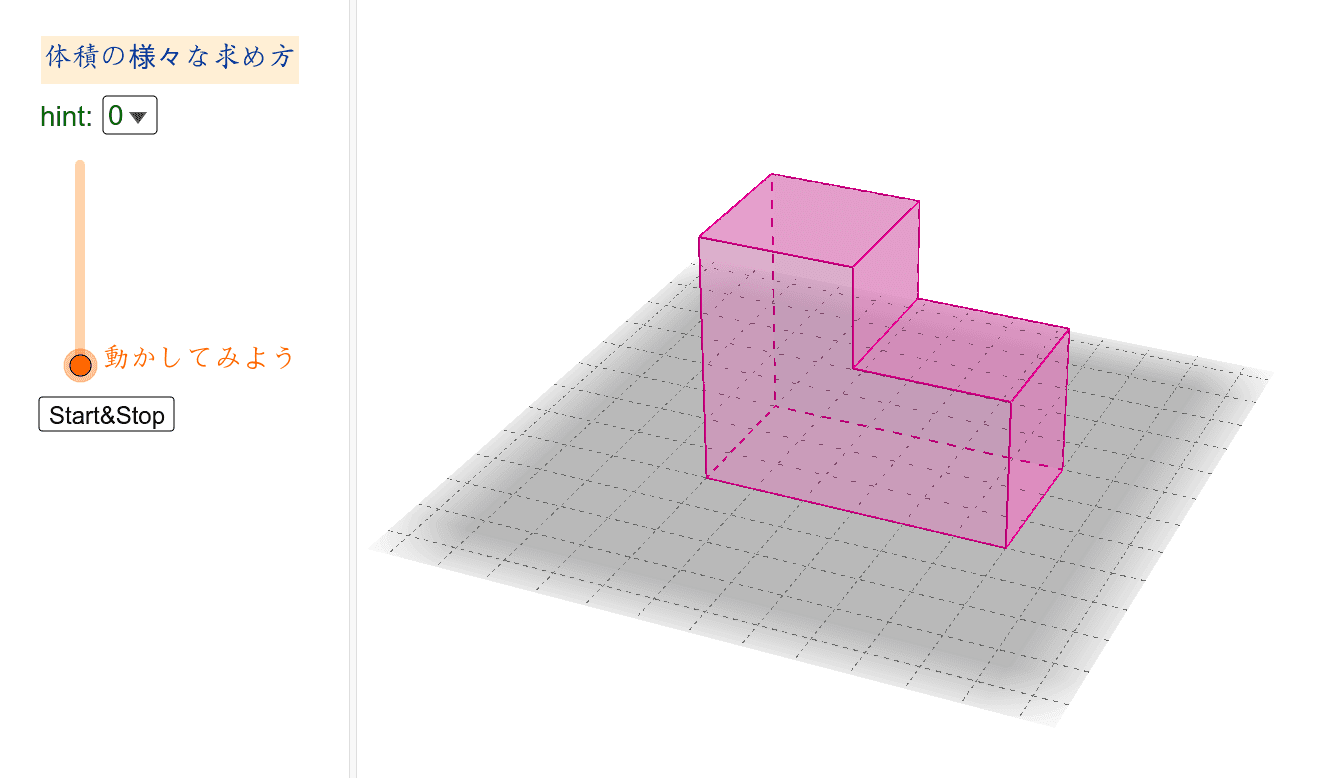



様々な体積の求め方 Geogebra




体積の求め方 計算公式一覧



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ
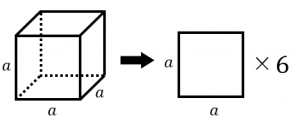



立方体と直方体の表面積を計算する 具体例で学ぶ数学



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




多くの教師が失敗する角柱の体積の求め方 算数を究める




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



1




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館
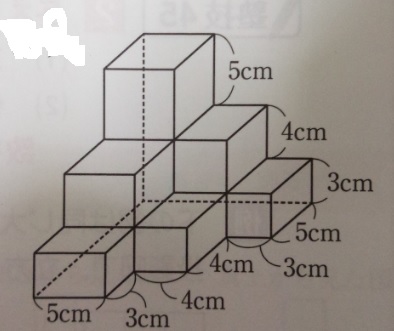



積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法



地図の体積計測



5年算数体積2わかる教え方



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座
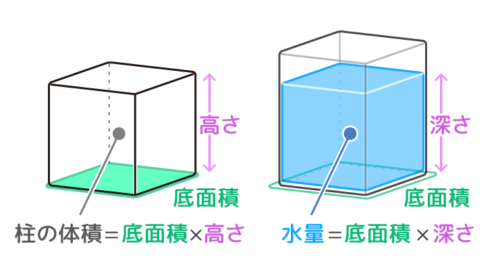



作成中 中学受験 容積 水の問題の解き方は 傾けたり物を沈めたり そうちゃ式 受験算数 2号館 図形 速さ
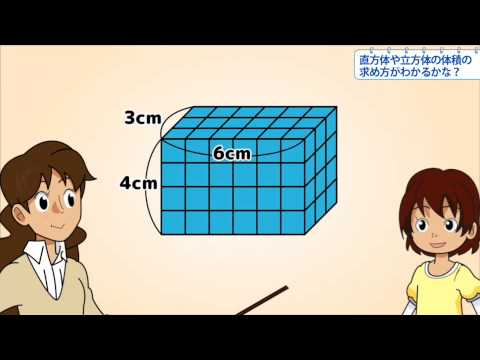



小5算数 直方体や立方体の体積の求め方がわかるかな Youtube
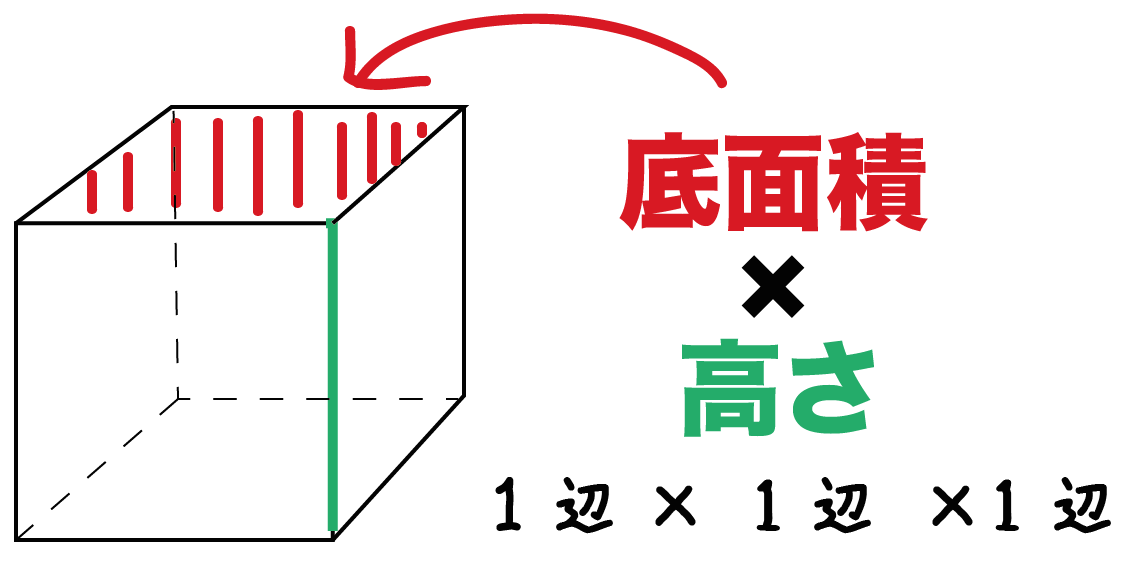



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 立方体 長方体 小学生 算数のノート Clear




体積 直方体 立方体 5 算数 算数 問題 算術



Math 積み重ねた立方体の表面積 働きアリ




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題
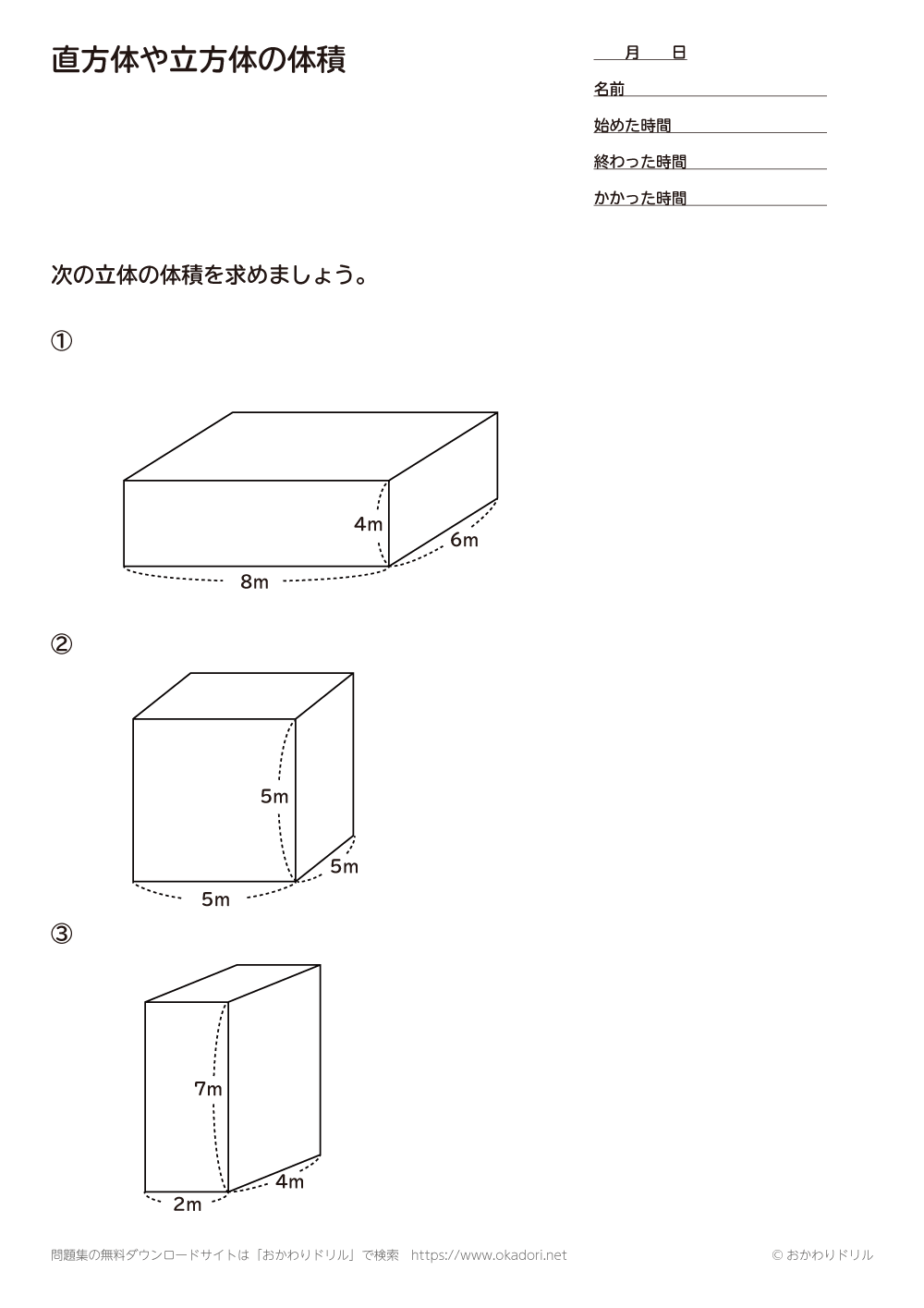



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
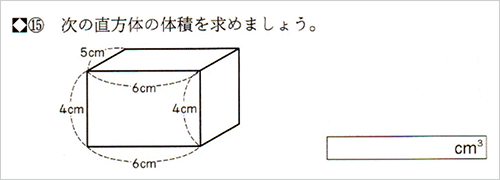



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




どうして1 3なの 錐の体積の公式の求め方 まなべーと
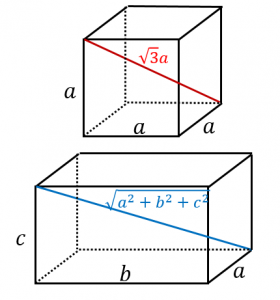



立方体と直方体の対角線の長さ 具体例で学ぶ数学



0 件のコメント:
コメントを投稿