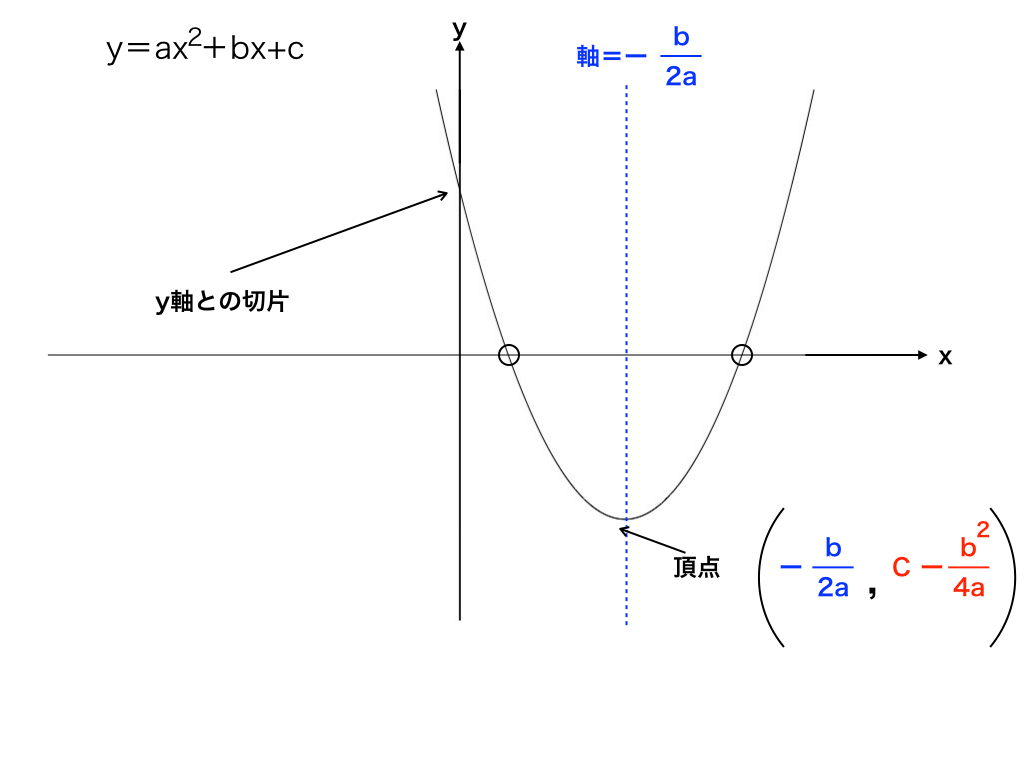
2次関数 $y=ax^2bxc$ のグラフは \begin{align} y=&ax^2bxc\\ =&a\left\{x^2\dfrac{b}{a}x\right\}c\\ &\quad\blacktriangleleft x^2の係数でくくる\\ =&a\left\{\left(x\frac{b}{2a}\right)^2\frac{b^2}{4a^2}\right\}c\\ &\quad\blacktriangleleft 平方完成\\ =&a\left(x\frac{b}{2a}\right)^2\frac{b^2}{4a}c\\ &\quad\blacktriangleleft \{~~\}をはずす\\・y=ax 2 q のグラフ ↓ →例題 ↓ y=ax 2 q のグラフ y=ax 2 q のグラフを y=ax 2 のグラフと比較しながら考えてみます。 やはり表を作ってみることが大切です。 下の表は 2x 2 と 2x 2 1 を比較したものです。 xのどの値においても, 2x 2 1 の値は 2x 2 の値に1を足したものです。 したがって, y比例の式 y=ax(aは比例定数) の式を、グラフで表すときのポイントは、次の通りだよ。 POINT 実際にy=2xなどの式がどんなグラフになるか、例題を通して確認しよう。

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ
Y=ax二乗 グラフ
Y=ax二乗 グラフ-Y = ax2 y = a x 2 2乗に比例 y y が x x の関数であり、 x x と y y の間に y = ax2 y = a x 2 という関係式が成り立つとき、 y y は x x の 2 2 乗に比例する という。 ただし、 a a は 0 0 でない定数で、比例定数といいます。 「 y y は x x の 2 2 乗に比例する」と問題文に実験データなどの誤差を含んだ値から, 最もフィットする関数を計算する手法が最小二乗法(method of least squares)です. 位置をとり,これをグラフにしてみます (説明のため,グラフ中では横軸を x,縦軸を y と書いてい 直線は1次関数ですから y = ax




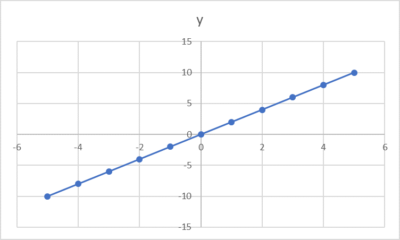
2次関数のグラフと直線
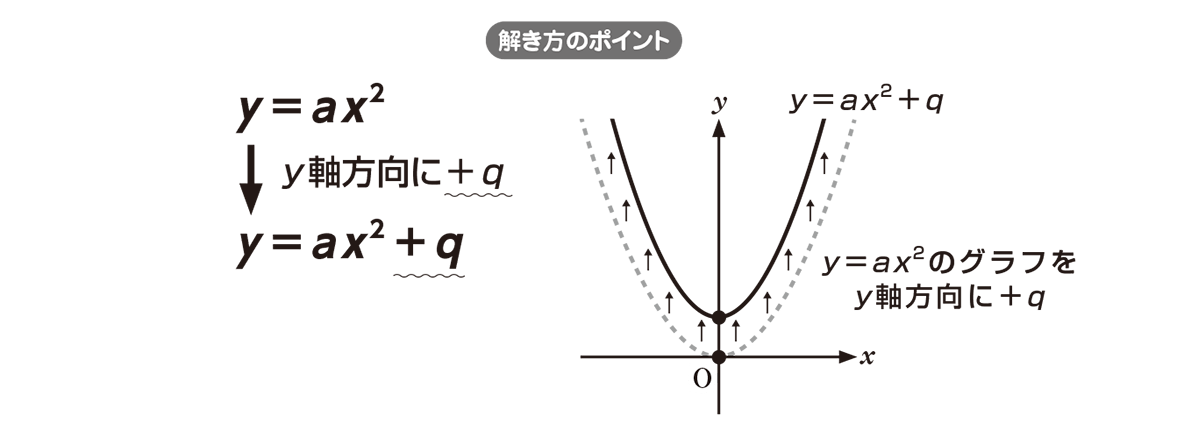
・グラフの性質 ・変域の求め方 誤字脱字があったらごめんなさい。 ระดับชั้น Junior High3, Textbook 新編 新しい数学3 東京書籍, Unit 関数y=ax^2, Keyword y=ax二乗関数グラフ GeoGebra x y z π 7 8 9 × これが、すべての x について成り立つので、「 y = x2 2 y = x 2 2 のグラフは、 y = x2 y = x 2 のグラフを y 軸方向に 2 2 だけ平行移動したもの」ということができるんですね。 一般的に、次のことがいえます。 y = ax2 q y = a x 2 q のグラフ y = ax2 q y = a x 2 q のグラフは、 y = ax2 y = a x 2 のグラフを y 軸方向に q だけ移動したものである 基本二次関数 y=ax^2 のグラフ
・グラフの性質 ・変域の求め方 誤字脱字があったらごめんなさい。 学年 中学3年生, 教科書 新編 新しい数学3 東京書籍, 単元 関数y=ax^2, キーワード y=ax二乗2次関数のグラフの平行移動 y=x²4x9 ここでは、この関数のグラフをx軸方向に4、y軸方向に−2平行移動したときに得られる放物線の方程式を求めてみましょう。 "y=ax²bxc"のグラフをx軸方向にp、y軸方向にq移動するというタイプの問題では、2通りの解き方 まずはグラフの形を判断することが大事! \(y\)の変域に注目すると、\(0≦y≦12\)ということでプラスの値になっていることが分かります。 このことからグラフは、 上に開いた形になるということがわかります。
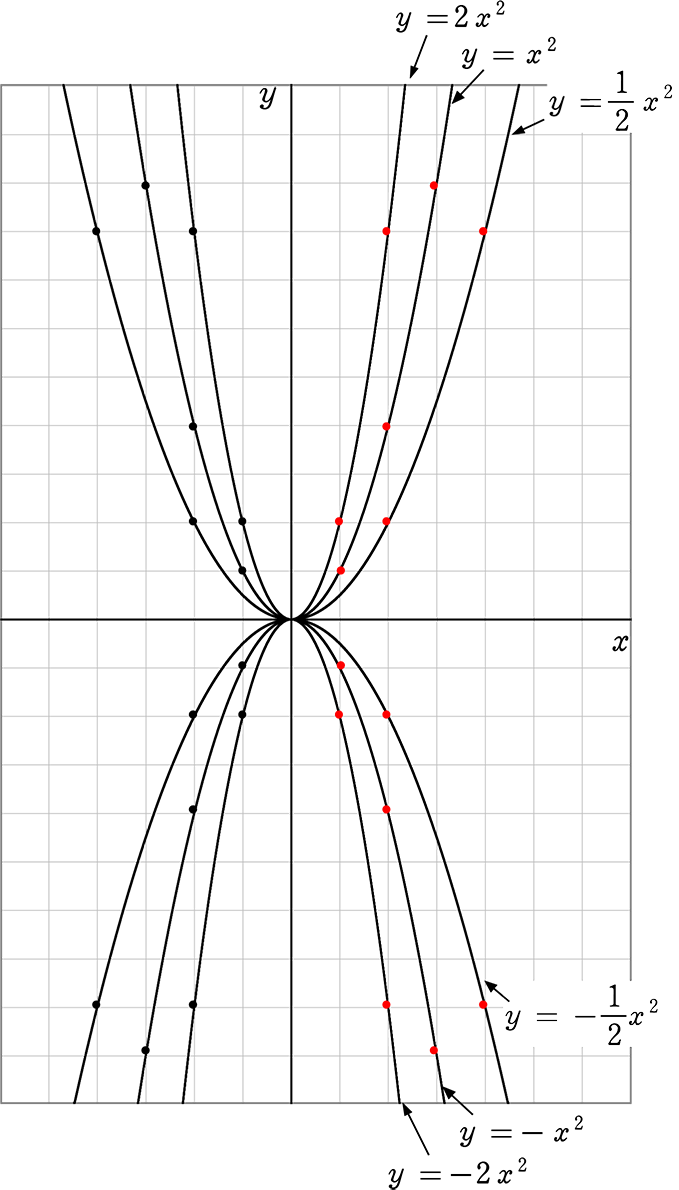
関数y=ax 2 上の2つの点B,Cがあるとして,それらのx座標がb,cだったとすると,直線BCの式は y=a (bc)xabc ・・・ (*) になるのです。 このことも後々で証明しようと思いますが,今は代入して触れるだけで。 本問の場合, ,b=2,c=4なので,これをそのままここでは,関数y=ax2 のグラフとその特徴について学習してみましょう。 関数y=ax2 において,x=k,-kのときのyの値をそれぞれ求 めると,ともに y=ak2, ya k ak=-=_i2 2 となるから, y=ax2 のグラフは 軸に関して対称であるといえます。最小二乗法は計測データの整理に使われる方法である。 n個のデータ(x 1,y 1),(x 2,y 2), (x n,y n)が得られたとする。 に最もフィットする直線をy=axbとすると、 でa,bが求められる。 以下詳しい解説が書いてあります。



中学数学 関数



1
y = ax2 y = a x 2 のグラフを 「放物線」といいました が、 y = ax2 bx c y = a x 2 b x c のグラフも 放物線 と呼びます。 形が同じなので、同じ名前で呼ぶんですね。 「二次関数 y = ax2 bx c y = a x 2 b x c のグラフ」のことを「放物線 y = ax2 bx c y = a x 2 b x c 」と呼びます。 また、 y = ax2 bx c y = a x 2 b x c をこの 放物線の方程式 と呼びます。① ax 2 bxc>0 ② ax 2 bxc≧0 ③ ax 2 bxc2次関数y=xの2乗+ax+bのグラフをx軸方向に-1、y軸方向に2だけ 平行移動すると頂点の座標が(-2,6)になるように、定数a、bの値を 求めよ!をどうか今日中にお願いします 質問<1347>りさぴょん「最小値が与えられた二次関数」



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download



2次関数のグラフとx軸の共有点 と 2次方程式の解 数学 苦手解決q A 進研ゼミ高校講座
図の放物線lはy=ax 2, 放物線mはy= 1 8 x 2 のグラフである。 直線x=4とそれぞれの放物線l,mとの交点をA, Bとして、x軸との交点をCとする。入力x,出力yとが直線関係にあれば次式で表される。 ここで, a, b は任意の定数である。 n 組の測定データ: 最も良く当てはまる直線は, y i と ax i b との差の2乗の和が 最小となる a と b の場合である。 y ax b 2)最小二乗法の計算 1 1 2 2 x y x y 関数y=ax2乗放物線グラフの書き方はこれでバッチリ! yはxの2乗に比例する関数 関数グラフ上の平行四辺形の座標、面積、二等分線などの問題を解説!




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



2次関数のグラフと係数
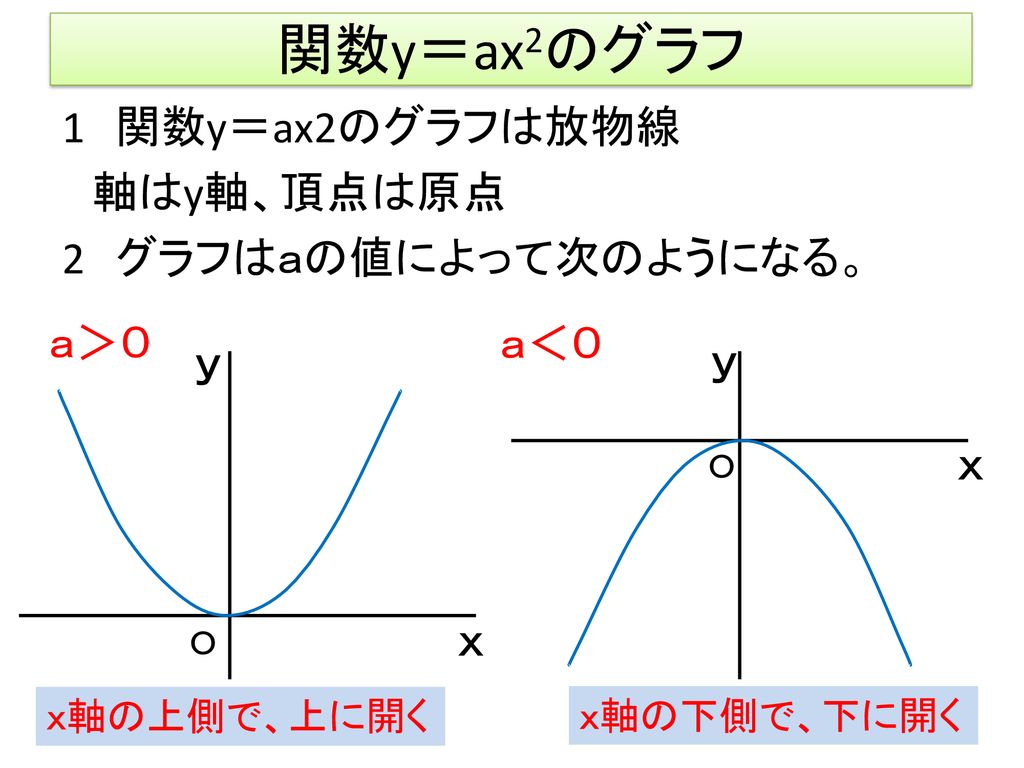
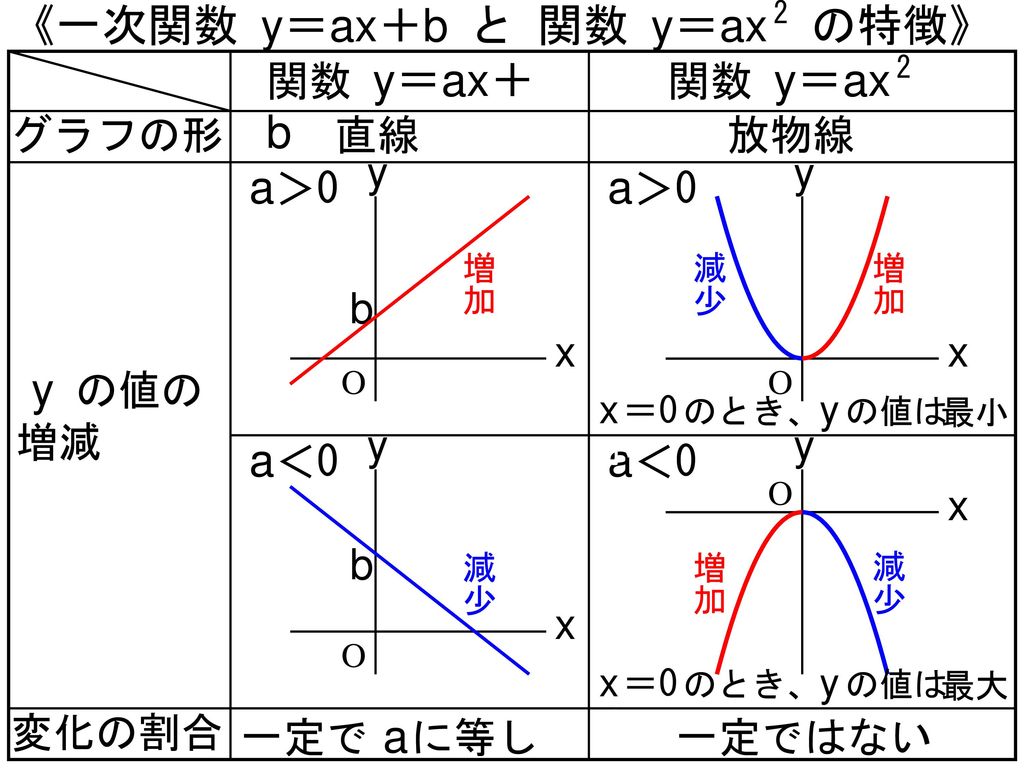
関数y=ax2 のグラ フとその特徴を 理解し,関数 ・y=ax2 のグラフの 特徴を見つけ,a の値との関係を 考える。 関数y=ax2 のグ ラフの特徴を調 べ,グラフをかこ うとしている。 a の値の変化と グラフの形を関 連付けて調べ, グラフの特徴を 放物線や軸,頂関数 関数y =ax2(2) 1 次の各問いに答えなさい。 (1)yはxの2乗に比例し、x=3 のときy =27 である。 ① yをxの式で表しなさい。 ② x=5 のときのyの値を求めなさい。 (2)関数y = ax2で,x=2 のときy = −8である。 ① aの値を求めなさい。 ② x= −4のときのyの値を求めなさい。 (3)yはxの2乗に比例 2乗に比例する関数のグラフの特徴の問題です基本のポイント 必ず原点を通り、その原点が頂点である y軸について対称である a > 0のときは上に開き、a < 0のときは下に開く aの絶対値が小さいほどグラフの開きが大きい y=ax2のグラフとy=ax2のグラフはx軸について対象である。




2次関数のグラフと直線




Aは関数y Ax二乗のグラフと直線y 3分の2x 4との交点 Bは直線y 3分の2x Clear
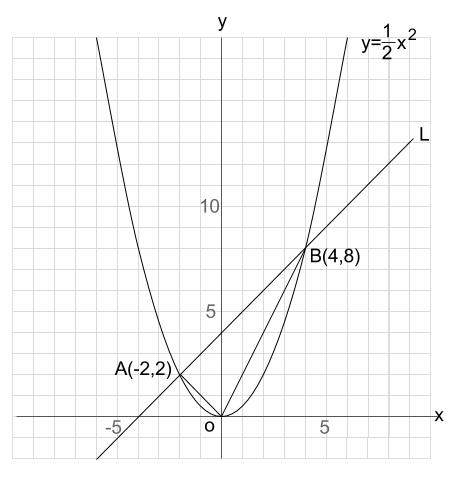
右図のように2次関数 y=ax 2 のグラフと直線 y=xb のグラフが2点A,Bで交わり,点Aの座標が (−2, 2) であるとき,次の問いに答えなさい. (1) 定数 a の値を求めなさい. (2) 定数 b の値を求めなさい. (3) 点Bの座標を求めなさい. (4) AOBの面積を求めなさい. 二次関数y=ax二乗... (1)のグラフは点A(4.2)を通っている。 y軸上に点BをAB=OB(Oは原点)となるようにする。 (1)Bのy座標を求めよ (2)∠OBAの二等分線の式を求めよ (3) (1)上に点Cを取り、ひし形OCADをつくる。 Cのx座標をtとするとき、tが・学校図書(問い・y= ・グラフ→x,y の関係が比例かどうか?) ・教育出版(問い・グラフ→枚数が100 枚ときに何段?) ・大日本図書(コラムでの説明) 風速x y の風が吹く時の、壁にかかる風圧を パスカルとすると、yはxに2乗に比例する〈変数・風速x と風 圧y〉




中3 数学 y Xの二乗の値の変化 中学生 数学のノート Clear



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
グラフの読み取り \(2\) 乗に比例(\(2\) 次関数)のグラフを読みとることも、非常に重要です。 例題1 下の図の放物線の式を求めなさい。 解答 原点を通る放物線なので、 放物線の式は \(y=ax^2\) となり2次関数のグラフは,放物線とも呼ばれ,ボールを遠投したとき描く曲線のような形をしています。 その曲線を式で書くと,y=ax2 (a≠0) の形に書かれます。 この章では,この曲線について,前の章で学んだ平行移動を行なうことにします。 まず,y=ax2 の性質と,これから使う名称について説明しておきます。 a は 0 以外の適当な数ですが,この値によって,グラフのY=ax 2 (a>0)のグラフは、図のように 「原点を通る、上に開いた放物線」 になるよ。 U字型 のイメージだね。 例題をいっしょに解きながら、実際にグラフが 「原点を通る、上に開いた放物線」 になることを確認していこう。



条件より2次関数の方程式を求める



無料ダウンロード Yax2 グラフ やもが
Y=ax 2 のグラフの特徴 必ず原点を通り、その原点が頂点である。 y軸について対称である。 a > 0のときは上に開き、a < 0のときは下に開く。 aの絶対値が小さいほどグラフの開きが大きい。 y=ax 2 のグラフとy=ax 2 のグラフはx軸について対象である。また,関数y=ax 2 はy軸を対称の軸にして左右対称ですので,2と4で,xの絶対値が大きい方がyの最大値をとることも考えましょう。 試しにx=2とx=4の両方を代入してみましょう。x=2のときはy=4a,x=4のときはy=16aになりますね。LINEST関数による最小二乗法の計算 Excelには、最小二乗法による直線フィッティング用にLINESTという関数が用意されています。 一般的な使い方は =LINEST(計算に使うYの範囲、計算に使うXの範囲、Y切片を0にするかしないか) というような形式です。 X,Yという順番ではなく、Y,Xという順番であることに注意してください。 範囲の指定の方法ですが という表があり




例題で学ぶ高校数学 Y Ax2



二次関数の最大 最小



Y Ax2乗 グラフの特徴と書き方をイチから解説します 中学数学 理科の学習まとめサイト




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks



人気ダウンロード 関数yax2乗 グラフの利用 ニスヌーピー 壁紙




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント



数学 二次関数が簡単になる解き方とグラフの書き方 札幌市 学習塾 受験 チーム個別指導塾 大成会



2次関数のグラフと係数




基本 二次関数y A X P 2のグラフ なかけんの数学ノート




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




二次関数y ax 2 のグラフは点a 4 2 を通っている y線 数学 教えて Goo



文字係数2次関数の頂点



二次関数のグラフと解の存在範囲の問題をわかりやすく解説



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット
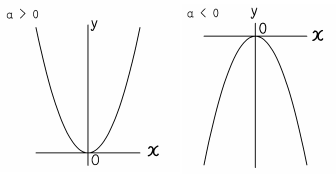



2乗に比例する関数 グラフ



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf
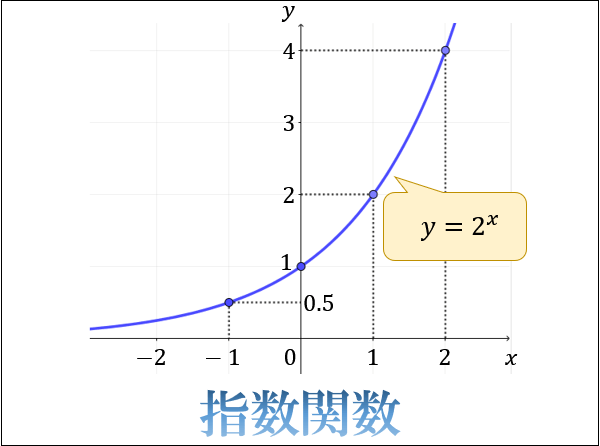



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート



Afsoft Website Afsoft Jp
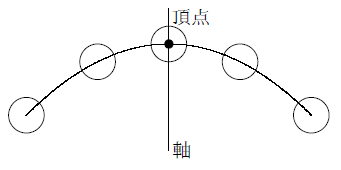



関数y Ax2のグラフ まなびの学園




2次関数のグラフ
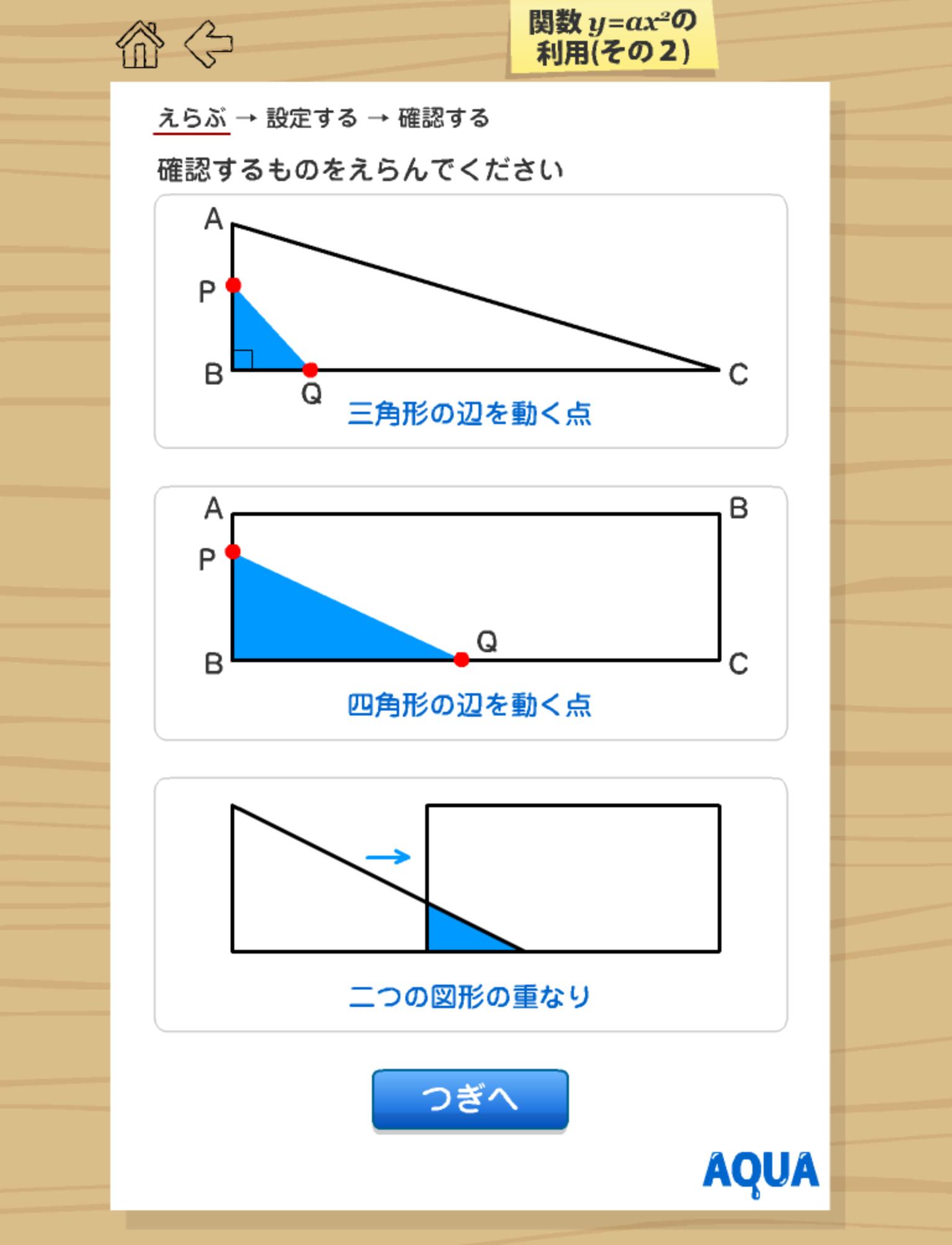



関数y Ax2の利用2 さわってうごく数学 Aquaアクア For Android Apk Download
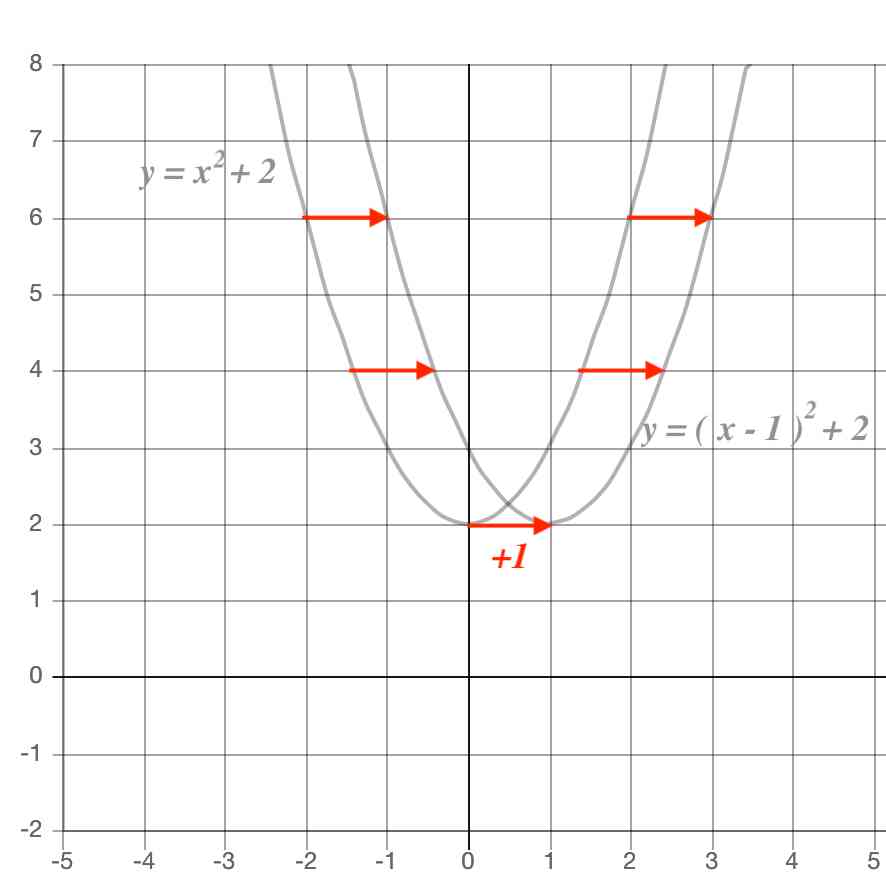



二次関数のグラフの書き方




スタディピア 関数とグラフ




Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト
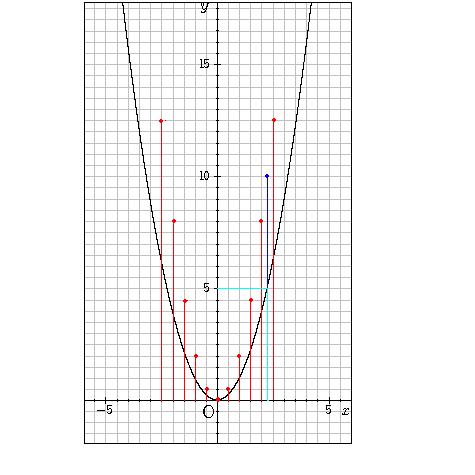



Y 2x 2のグラフ Takapの数学日記
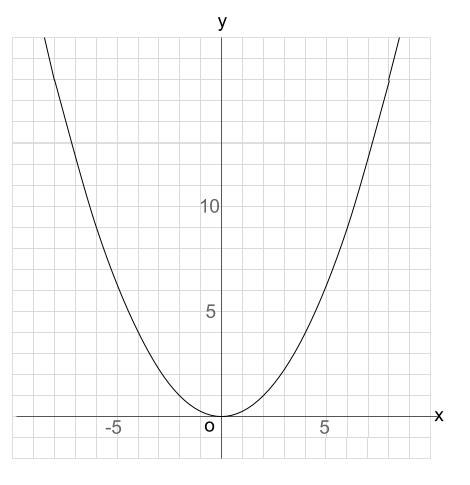



中学数学 Y Ax 2 のグラフを読み取る 中学数学の無料オンライン学習サイトchu Su



4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download
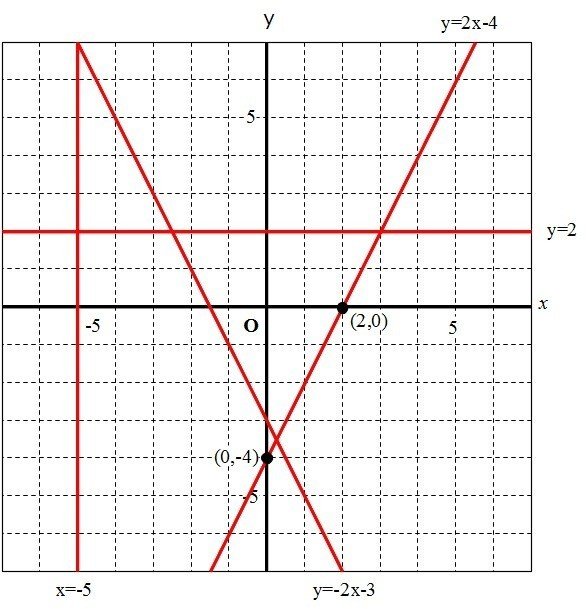



超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note



図の1のように 関数y Ax二乗のグラフ上に X座標が4 Y座 Yahoo 知恵袋




2次関数と直線の交点 基 標 数学の解説と練習問題




Y Ax 2 Bx C のグラフのかき方 事後テスト解答例 Kyokuryo Math




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks




例題で学ぶ高校数学 Y Ax2 Q




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube



1




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
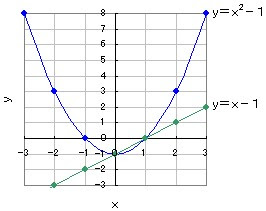



ベストyx2乗1 グラフ 最高のぬりえ




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



1
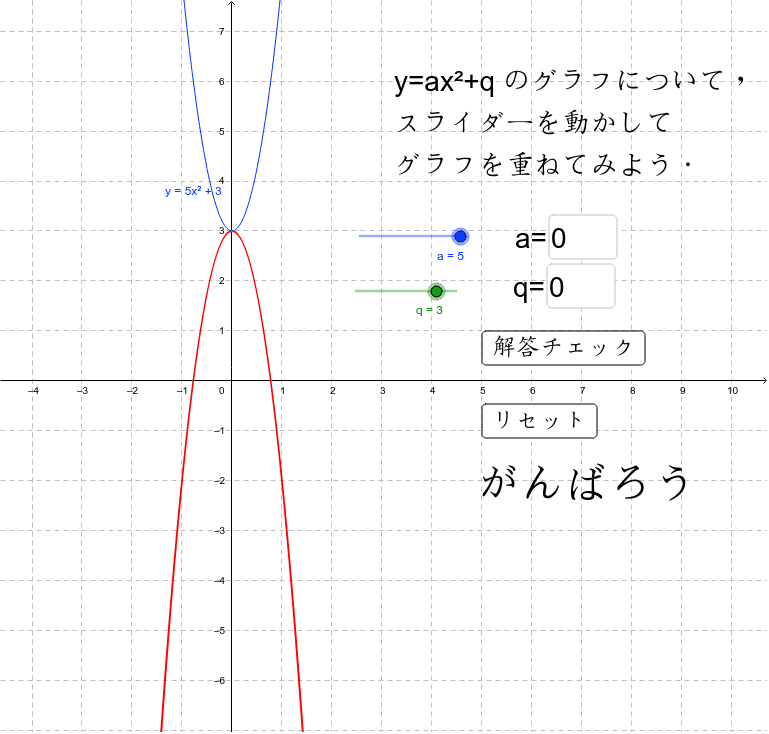



Y Ax 2 Qの関数のグラフの形 Geogebra



中3数学 関数y ax二乗 放物線と直線1 発展問題 問題 324 プリント



Y Ax 2




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ
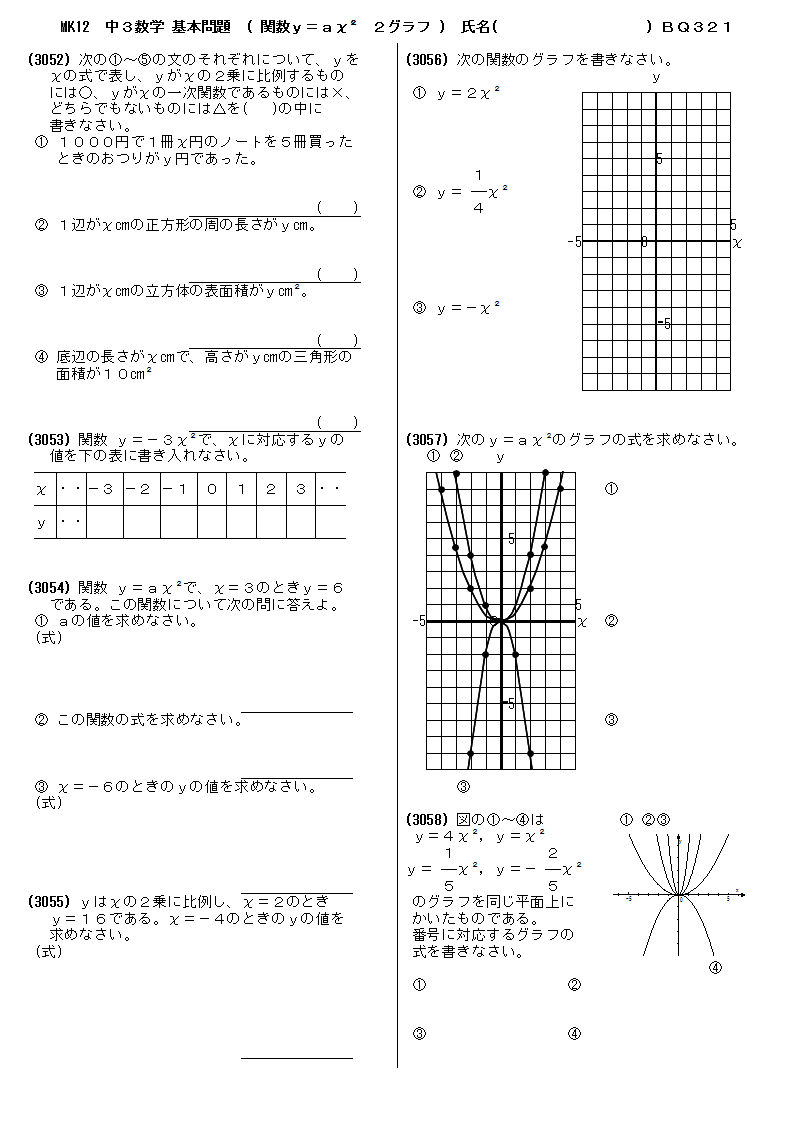



無料 中3数学 基本問題 問題プリント 321 関数y ax2 2グラフ



2乗に比例するグラフ 中学から数学だいすき



数学3年 2次関数 Y Ax2 2次関数のグラフ 2次関数の変域 2次関数の応用 2次関数のグラフ Xの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 問題4 正解4 解説
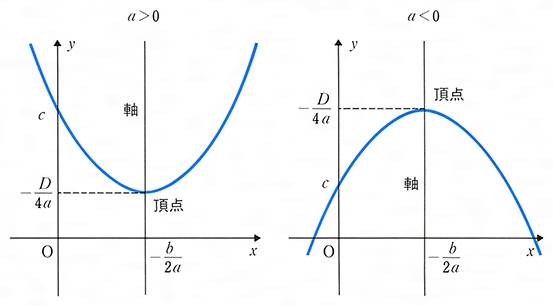



二次関数とは コトバンク




2 Yax2 79t03 Descubre Como Resolverlo En Qanda




Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア
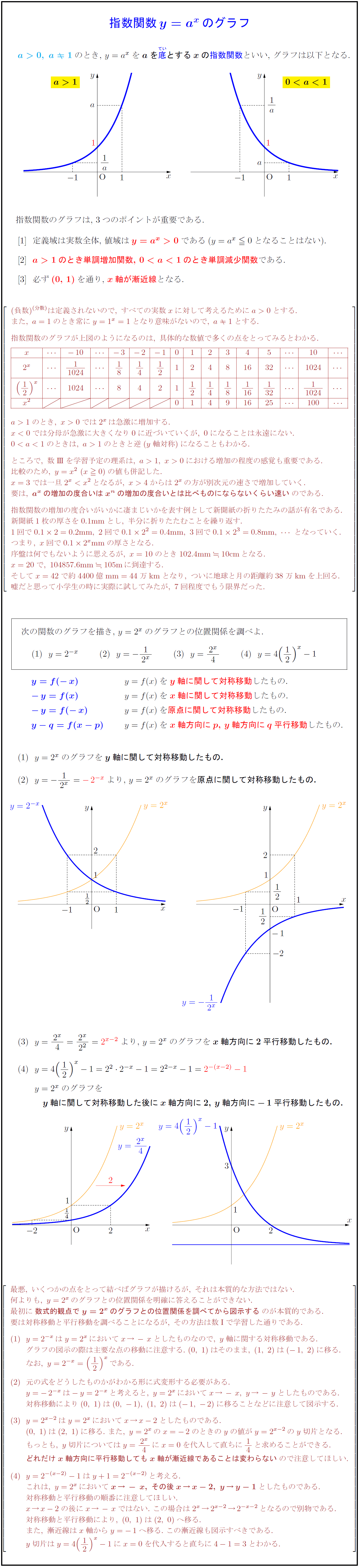



高校数学 指数関数y A Xのグラフ 受験の月



Y Ax 2




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext




Y Ax 2の変域 チーム エン




中3 関数 Y Ax2 まとめ 中学生 数学のノート Clear




例題で学ぶ高校数学 Y A X P 2




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター



図のように関数y Ax二乗 二次関数 のグラフ上に2点a Bがそれぞれの座標 Yahoo 知恵袋



辞書 二次関数のグラフの特徴 わかりmath
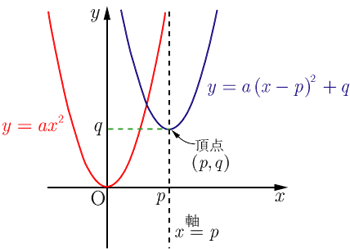



2次関数のグラフ Y A X 2 P Q



二次不等式とは 解き方や解の範囲の求め方 判別式の問題 受験辞典



関数y X 2のグラフの性質 勉強ナビゲーター
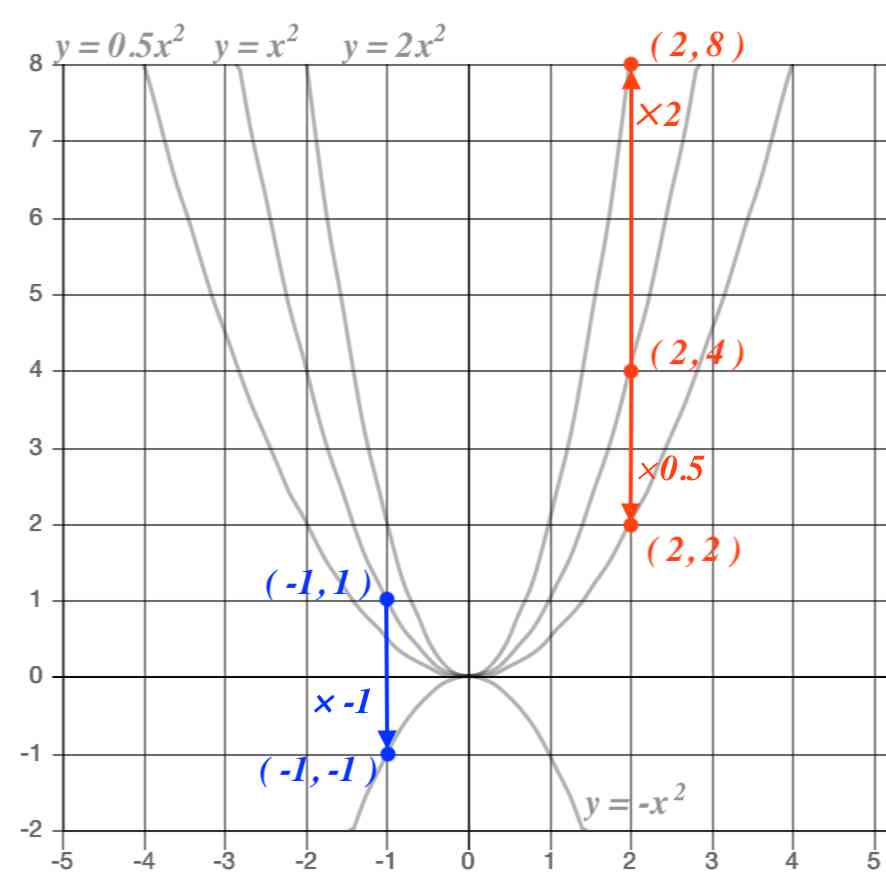



二次関数のグラフの書き方
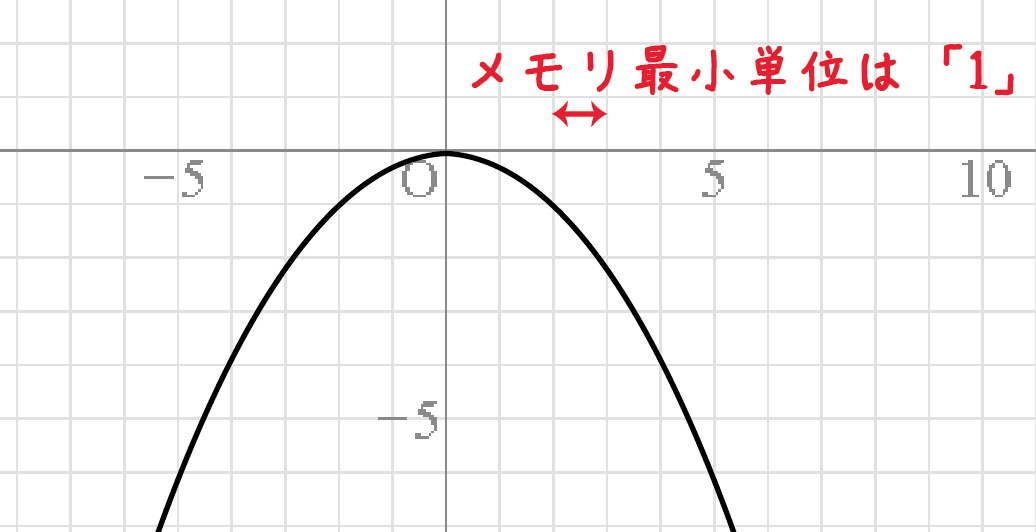



中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト
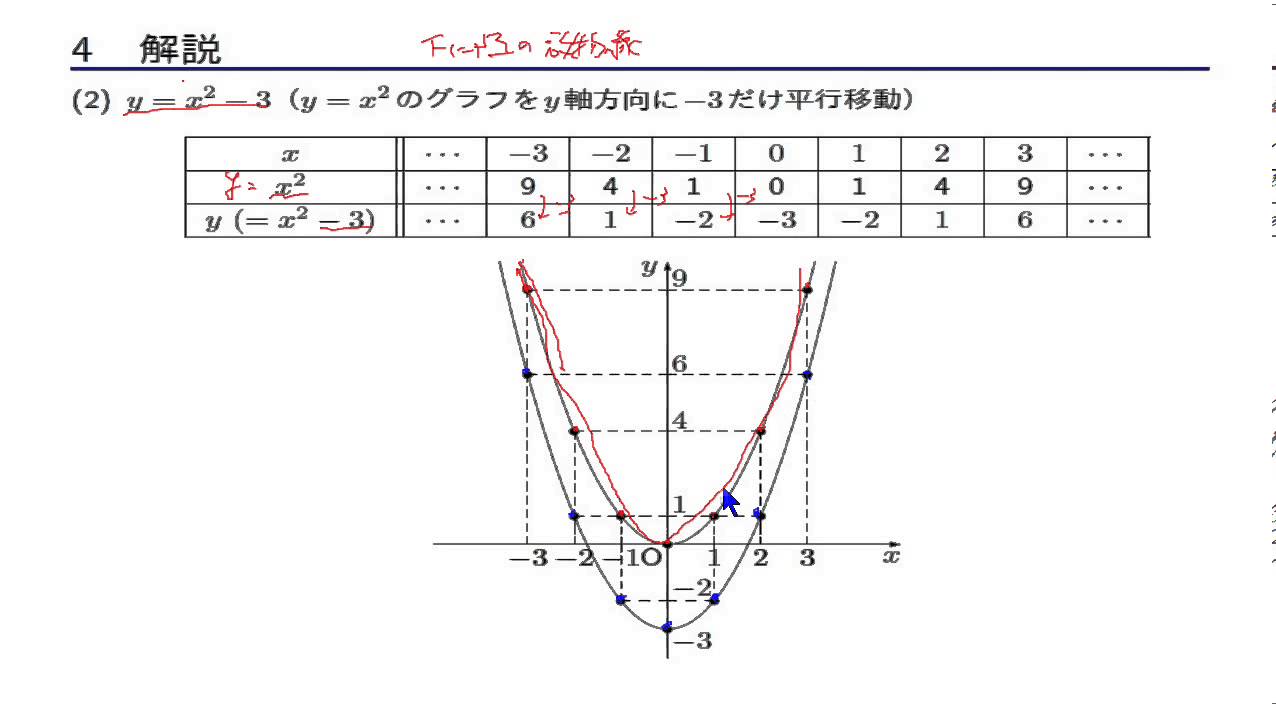



数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ
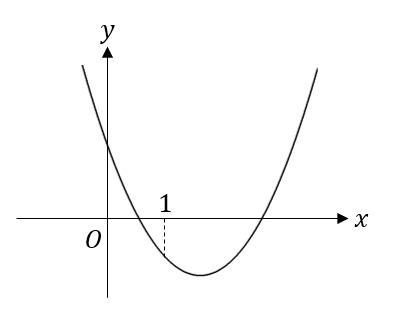



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い




Y Ax B 2x 1 1 のグラフが点 1 0 Okwave




二次関数とグラフ 中3数学 高校数学 Irohabook




2次関数 Y Ax Qのグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア




2次関数のグラフと方程式




数学 中3 35 二次関数のグラフ Youtube




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext
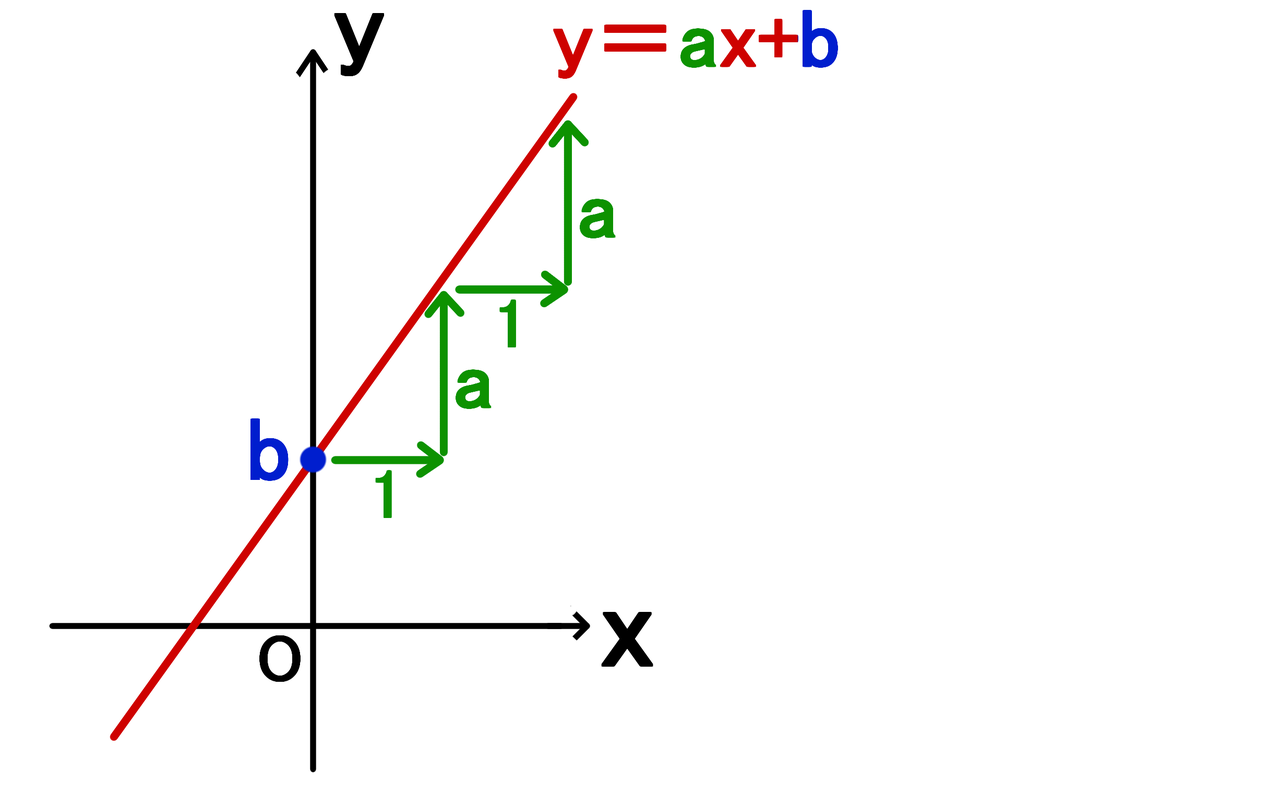



関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



1
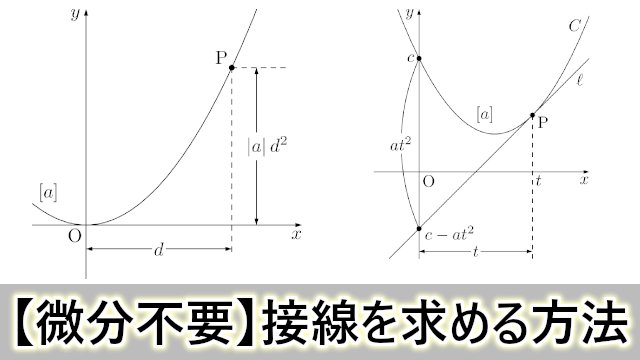



微分不要 放物線上にない点から放物線に引いた接線を簡単に求める方法 大学入試数学の考え方と解法




2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題




数学 2次関数 頂点の求め方 オンライン無料塾 ターンナップ
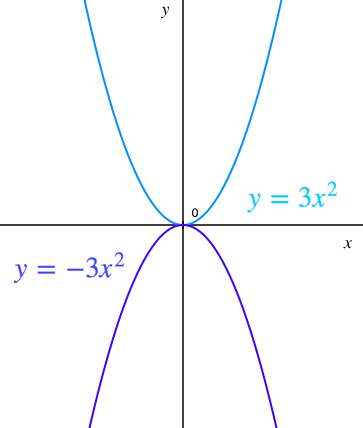



二次関数 放物線 確認問題 苦手な数学を簡単に




二次関数 Wikipedia



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf



授業実践記録



授業実践記録



0 件のコメント:
コメントを投稿