中学数学 1次関数 マイナスの増加量って何? 1次関数 変域の求め方 1次関数 傾きや切片が分数であるグラフのかき方 1次関数 直線の傾きを求める計算 1次関数 座標軸に平行な線分の距離 1次関数 直線の式を求めるときの適当な2中学2年生 数学 1次関数と連立方程式(文章題) 練習問題プリント 無料ダウンロード・印刷 中学2年生数学1次関数と連立方程式の問題を繰り返し練習できる教材プリントを無料ダウンロード・印刷中学2年生 数学 1次関数(文章題) 練習問題プリント 無料ダウンロード・印刷 ;
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
2 次 関数 中学
2 次 関数 中学- 2次関数の三角形の面積を求めるポイント 2次関数の三角形の面積を解くときは、『以下の図示の公式で解く』と言っても過言でないぐらいです。 鈍角三角形でも、同じようにこれを利用し解きます。 一般的には、頂点に向かって補助線を引き2つの三角形中学2年 中学3年 中学1年 1次関数y=ax+bはxが1進むと、yはa進む直線のグラフだということはわかるかな。 この直線のグラフでは、xの係数aの値が大きければ大きいほど、グラフの傾き具合も大きくなっていくんだ。
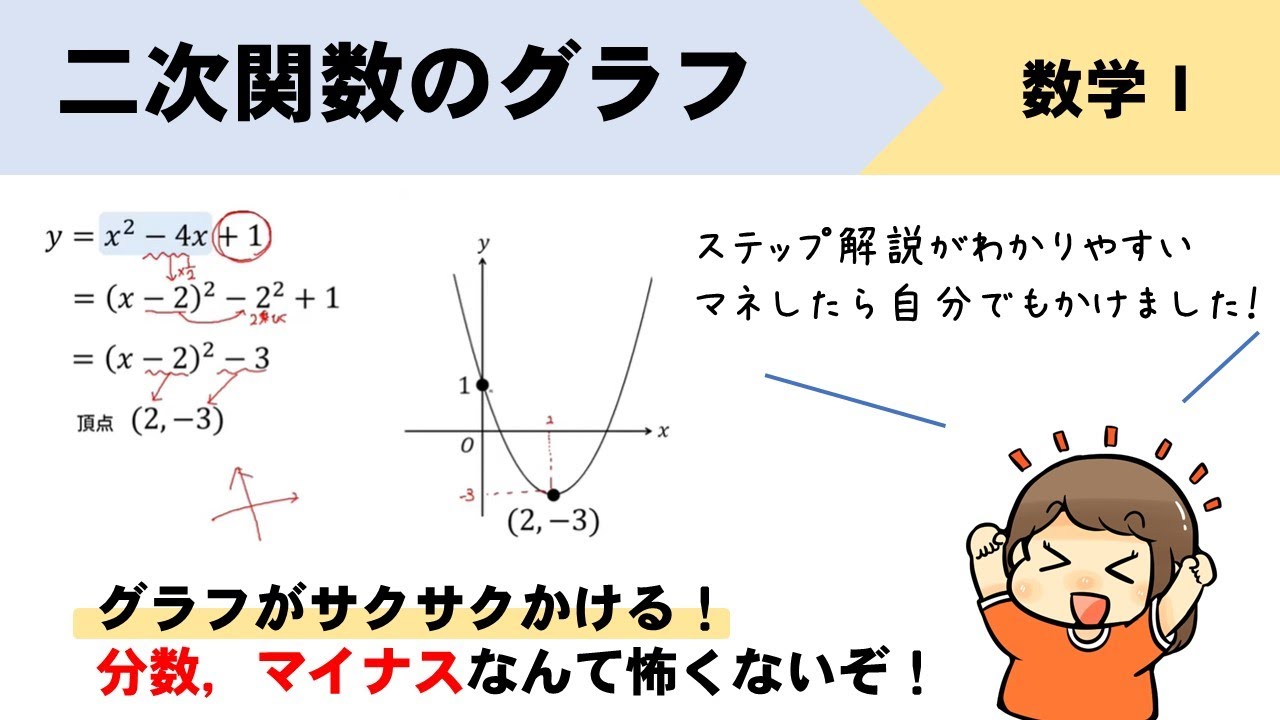



数学苦手な高校生向け 二次関数グラフの書き方を初めから解説 数スタ
中学2年生 数学 1次関数(文章題) 練習問題プリント 無料ダウンロード・印刷 教材の新学習指導要領への対応について ただいま、ちびむすドリル中学生では、公開中の中学生用教材の新学習指導要領(21この問題,大人には簡単だけど,中学生には2つぐらい苦労するポイントあります。 「関数と三角形の面積比率と文字式」 出典:平成29年度 北海道 高校入試 過去問 範囲:関数 難易度:★★★★☆ <問題> <PDF,解答例はこちら↓↓> » more Tweet comment () @ y=ax^2(2次関数)のグラフ 中点1次関数,2次関数,3次関数,三角関数,指数関数,対数関数,導関数 中学から高校の数学を指導するにあたって切っても切れない言葉.それが関数です. この記事のシリーズでは,関数指導に関する要点と指導のポイントを押さえていきたいと思います. 第2回目の本記事では,2次関数の
中学数学の実践編「2次方程式」を実際に解いてみます。 本書曰く、生活レベルで求められる数学的思考は中学数学で十分に養われるとのことですので、中学数学をマスターすることを目指します。 東大の先生! 文系の私に超わかりやすく数学を教えて2次関数とは、「2次の関数」、つまり「変数の次数が2の関数」を指します。 2次 関数を表す式:y = ax2 y = a x 2 比例を表す式は y = ax y = a x で x x は1次でしたが、この x x が2次になったものが2次関中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく 中学生がつまずきやすい数学分野 2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張 二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく 中学
2年 連立方程式 解と係数 (1)問題, (3)答b=5 (誤) b=3 (正) 1年 文字式の計算2 (加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5 (3)解答 (0,4)→ (0,4)または (0,4) 1年 文字式の計算3 (乗除) 答3③9c誤→49c正 1年 文章を等式にする 答 (9)12x→ 9 2 ⑥ 2元1次方程式と1次関数 ①(問題 中学2年生で学習する「確率」のテスト対策プリントになります。テスト前の復習として活用してもらってもいいですが、予習をして定着しているかどうかの確認のためにも利用してください。 スポンサーリンク 中学生必見!|数学の無料プリント~中3 2<中学2 年生> 3 1次関数 ① 1次関数 要点 演習 解答 ② 変化の割合 要点 演習 解答 ③ 1次関数のグラフ 要点 演習 解答 ④ 1次関数の 式の決定 要点 演習 解答 ⑤ 2元1次方程式 のグラフと交点 の座標 要点 演習 解答 ⑥ 1次関数




二次関数の式と値の求め方 2 現役塾講師のわかりやすい中学数学の解き方
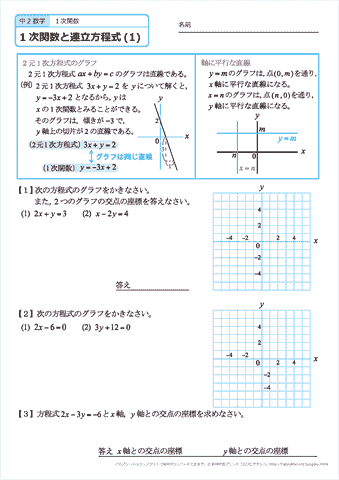



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
変化の割合と交点 2次関数における変化の割合と、2次関数上の三角形の面積の求め方や2等分線について学習します。 変化の割合 三角形の面積 三角形の2等分線 変化の割合と交点 変化の割合と交点 変化の割合と交点 変化の割合と交点 二次関数嫌いの先入観を解消するには、「 二次関数は一次関数から1つ増えただけ 」と思うことが大切です。 一次関数を発展させたのが二次関数です。 一次関数は、例えば「 y=ax 」です。 a に「 2 」を入れれば「 y=2x 」になります。 これが簡単なのは、「 y は x の 2 倍」とすぐに理解 2次関数の特徴 \(y=ax^2bxc \quad (a \neq 0)\)について \(\begin{align}① \quad & a \gt 0 の時、下に凸。 \\ & a \lt 0 の時、上に凸。\\ \end{align}\) \(\begin{align}② \quad & a \gt 0 の時、最小値がある。 \\ & a \lt 0 の時、最大値がある。 \end{align}\)




超簡単 二次関数の頂点の求め方 平方完成と公式 2つを慶應生が解説してみた 練習問題付き 高校生向け受験応援メディア 受験のミカタ




数学 中3 42 二次関数の利用 一次関数との交点編 Youtube
2 二次関数の表は x 2 に比例する 21 二次関数は放物線のグラフになる 22 a の値でグラフの形が変わる 23 a > 0 で下に凸になり、 a < 0 で上に凸になる3年2次方程式総合問題Lv2 2(2)①と②の答が逆になっていたので訂正しました。 19/9/4 3年円周角6 ⑥答127°(誤)→ 117°(正) 19/8/30 3年2乗に比例する関数 変域3 2(4)答t=6(誤)→ t=0(正) 19/8/28 3年 2次方程式総合問題Lv3 3(2)図の記号が間違っていました。 中2数学「一次関数の式を求めること(傾きと1点の座標がわかるとき)の問題」です。1次関数y=axbにおいて、 aの値がわかるとき → 傾き、変化の割合、平行な直線がわかっている場合 bの値がわかるとき → 切片がわかっている場合以上が




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット
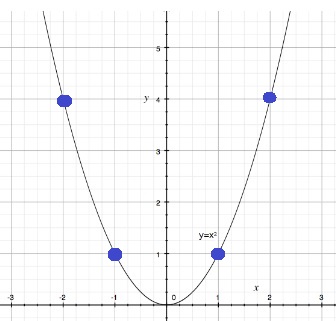



数学 中学3年生 二次関数の解き方 教え方のコツ グラフの書き方 なるほど 塾講師が教える教え方のコツ
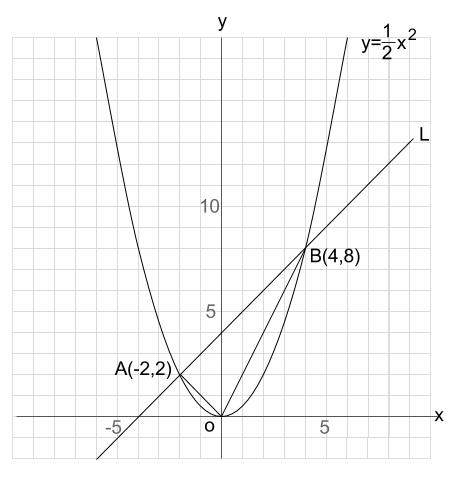
二次関数の標準形というのは、 \begin{align} y = a(xp)^2 q \quad \text{\(a\)は\(0\)ではない)} \end{align} 例 という書き方になっているものです。 一般形で書かれた式は、必ずどんな式でも標準形に書き直すことができます。 ただし、そのためには一工夫が必要になり、その工夫が平方完成という式中学 数学 2次関数(中学)三角形の面積を二等分する直線の式 更新日: 15年4月7日 スポンサードリンク 例題 原点をoとし,関数 のグラフ上に,x座標が2となる点aと,x座標が4となる点bをとる。 (1)直線abの式を求めなさい。 (2) oabの面積を求めなさい。 (3)点aを通り, oabの面積を2等分する2次関数y=ax^2のポイントは! y=ax^2になっているとき、yはx^2に比例するという 「yはx^2に比例する」と言われたら、「y=ax^2」とおく y=ax^2の「a」を
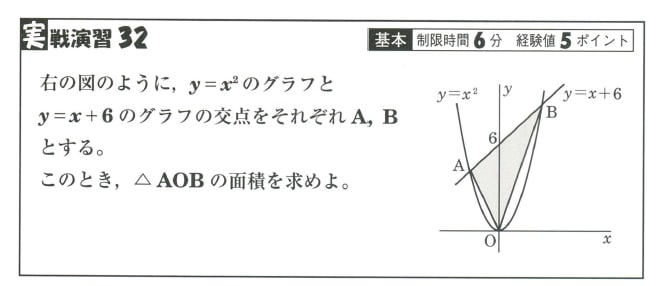



中学数学 1次関数 2次関数 32 福岡県 熊本県 高校入試問題 英語 数学 さくら教育研究所 中学 高校受験 Skredu



1
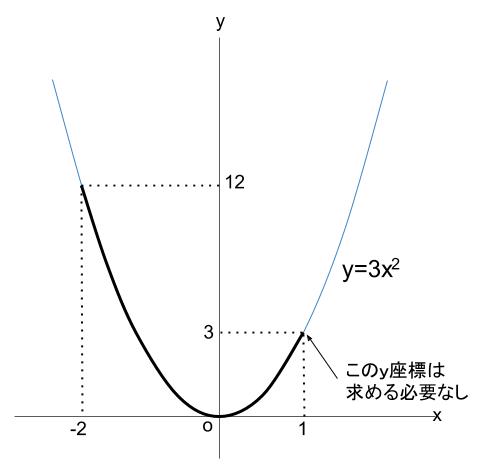
①1次関数と反比例,②2次関数,③動点p ①,1次関数,反比例グラフ ・最初の等積変形(★★☆☆☆)(オリジナル) 実は等積変形でなくても解けるのですが,まあ練習用に。 ・順序だてて(★★☆☆☆)(オリジナル) 関数記述対策の初めの方に。 ・1次関数と合同と高さの比 2次関数のグラフの特徴 練習問題 次の問いに答えなさい。答えは、次の関数の中からすべて選び、記号で答えよ。 (ア)y=x 2 (イ)y=2x 2 (ウ)y=3x 2 (エ)y=1/4x 2 (1)yの値がつねに0以下である。 (2)グラフが関数y=3x 2 のグラフとx軸について対称である。変化の割合のポイントは! 変化の割合とは、x の増える量に対して、y がどれだけ増えたかを示す割合で、( y の増加量 ) / ( x の増加量) で求める



2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター



2次関数 グラフ 中学から数学だいすき
中学数学1次関数 式の決定 中学数学2直線の交点(連立方程式とグラフ) 中学数学1次関数と三角形の面積・その1 中学数学1次関数と三角形の面積・その2 中学数学1次関数 ばね 中学数学1次関数の利用 線香 中学数学1次関数 動点 中学数学で習う「関数」の例! xの関数であるyの具体例を紹介しよう。 中学1年生では、 y = 2 x のようなシンプルな関数が登場するよ。 この関数のxに数字の「2」を入れてあげるとyの値は「4」になるし、 xに「3」を入れると、yは「6」になるね。中学関数グラフから長さを求める方法を基礎から解説! yはxの2乗に比例する関数 変化の割合二次関数y=ax2の裏ワザ公式?
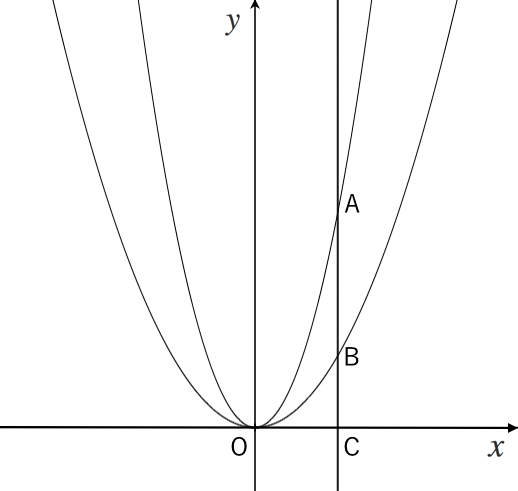



二次関数の利用 グラフ系の問題 苦手な数学を簡単に




中学数学問題集 中3 2次関数 18 4 中学数学高校数学個別指導in山形市 数専ゼミ
2次関数 2乗に比例する関数(基本) 解答 ① 2 ② ③ ④ ⑤ 2 2 8 y x y=6x y= 48 x y=3x5 y= 800 x 1 y=πx 無料で使える中学学習プリント関数と図形(面積を二等分する直線) 解説 頂点を通る直線で三角形の面積を二等分する p q r 頂点とその対辺の中点を通る直線は三角形の面積を二等分する。 中点を求める ≫ 2点から直線の式を出す ≫ 図でa(8,8),b(12,0)である。 x y a b o (1)点oを通り aobの面積を二等分する直線の式を求めよ。 (2)点(※ 「二次関数」以降の計算式を習う学年は高校なので(17年現在では)、中学生はまだ覚えなくていい。) なお、二次関数の一般式は = である。 二次関数の式やグラフからも分かるように、二次関数はもはや比例式ではない。 高校では、数学や理科



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平成25年長野県立高校 入試問題 二次関数の変域の問題の解き方 現役塾講師のわかりやすい中学数学の解き方
変化の割合 変化の割合= yの増加量 xの増加量 比例反比例、1次関数、そして2乗に比例する関数、 変化の割合 はすべて同じ式を用いる。 ただし、1次関数では変化の割合は一定だが、 2乗に比例する関数では変化の割合は一定にならない。 y=3x 2 についてそれぞれの場合の変化の割合をもとめる。中学2年生のときに、1次関数については学んだよね。 yとxについて 「y=ax+b」 (aとbは具体的な数字)の式が成り立つときに、 1次関数 と呼んだね。 これから学習するのは、式がちょっとバージョンアップした 「関数y=ax 2 」 。Y=ax2のグラフ1③ 1 A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 ③ A(6, 9), B(1,3) A(6, 9) B(1,3) ←点Aを通るとき ↓aの絶対値が大きいほど 開き方が小さい x y O aの絶対値が小さいほど ↓開き方が大きい y=ax 2 のグラフは,




中学3年の数学 動画 二次関数の利用 一次関数との交点編の問題 19ch




中学数学の2次関数 Y A X 2 大垣日本大学高校の入試問題を解く 身勝手な主張




世界一わかりやすい数学問題集中3 4章 二次関数
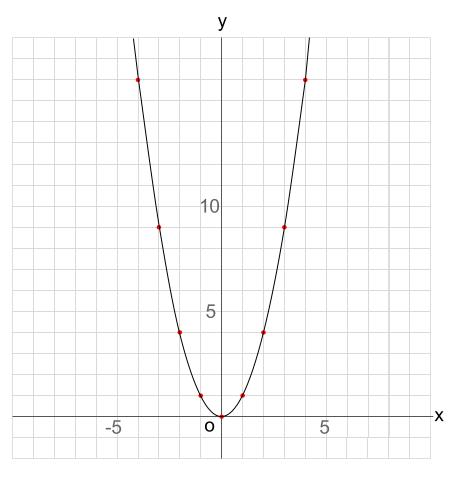



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su
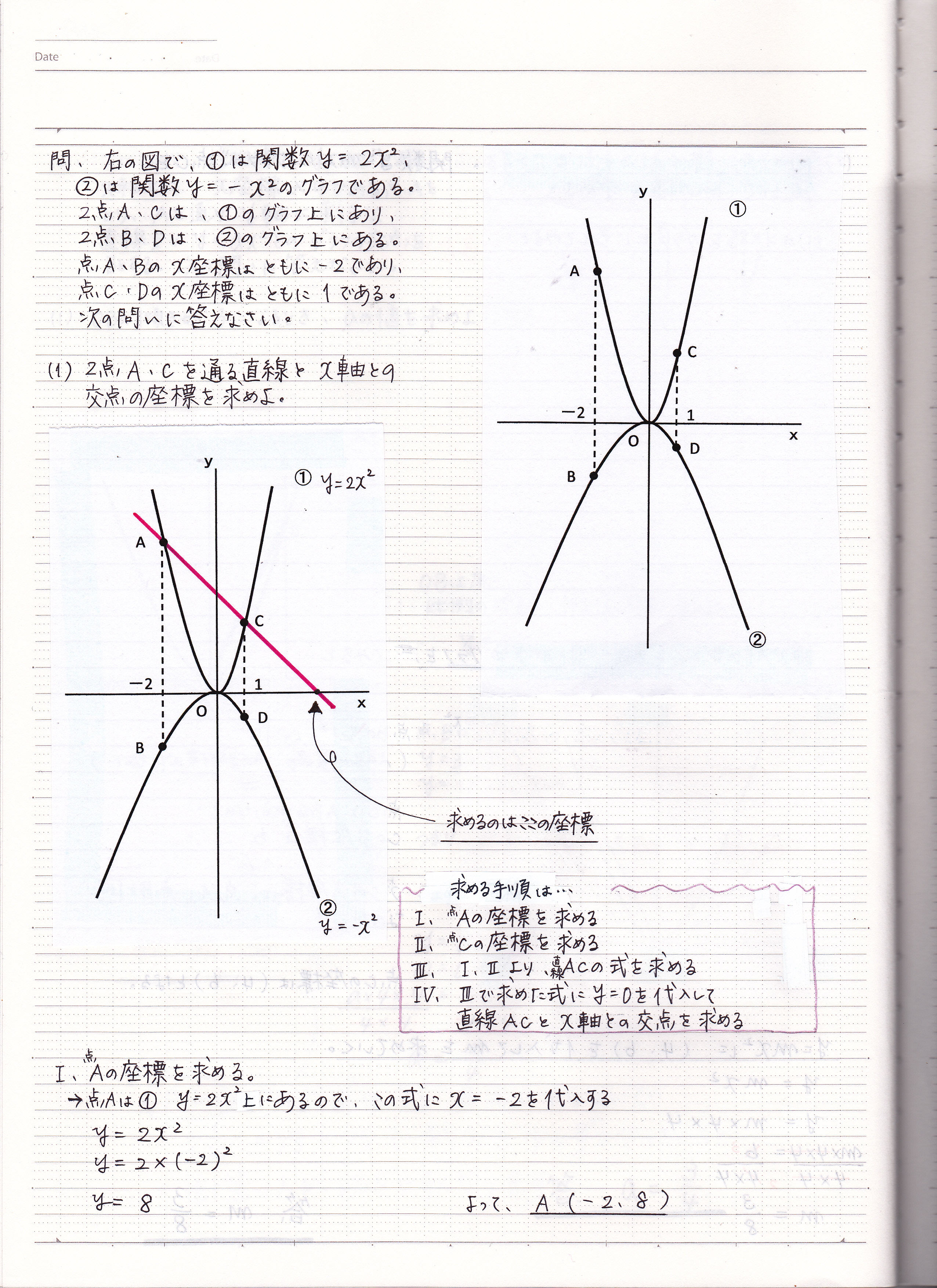



二次関数の利用 現役塾講師のわかりやすい中学数学の解き方




二次関数の利用の問題の解き方 グラフ無 はやさ 1 現役塾講師のわかりやすい中学数学の解き方




中学3年の数学 動画 二次関数の利用 一次関数とのコラボ編の問題 19ch




中学数学 放物線と直線の組み合わせで使える裏ワザ ジャムと愉快な仲間たち 0名



中学の一次関数 2次関数の勉強のコツを知って得意になろう



二次関数の利用 グラフ系の問題 苦手な数学を簡単に



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス




中学数学 二次関数の台形の二等分線を求める練習問題 Pikuu




2次関数のグラフと直線




中3数学 2次関数のグラフの特徴と練習問題




二次関数の三角形 等積変形を使ったパターンの解き方 Qikeru 学びを楽しくわかりやすく




中3数学 二次関数クルクル回る問題 ブログ アビット



U9j580gf8iba369ji2w Xyz P 794
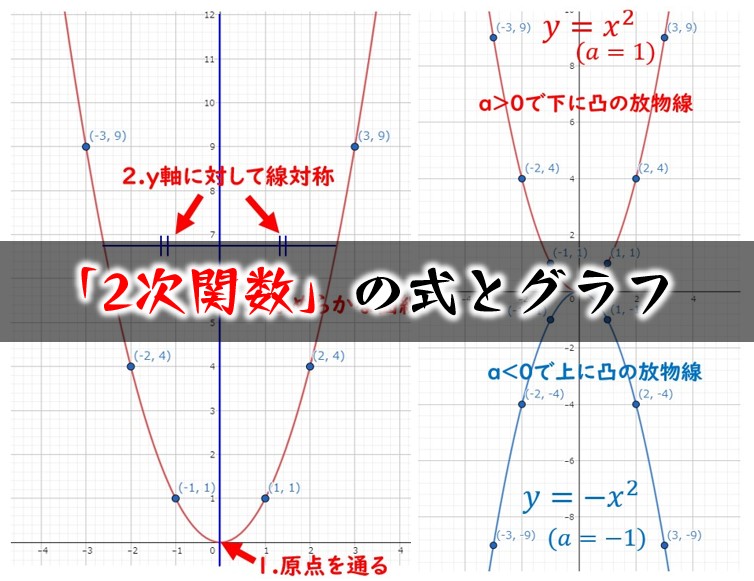



2次関数とは 式とグラフの解説 数学fun
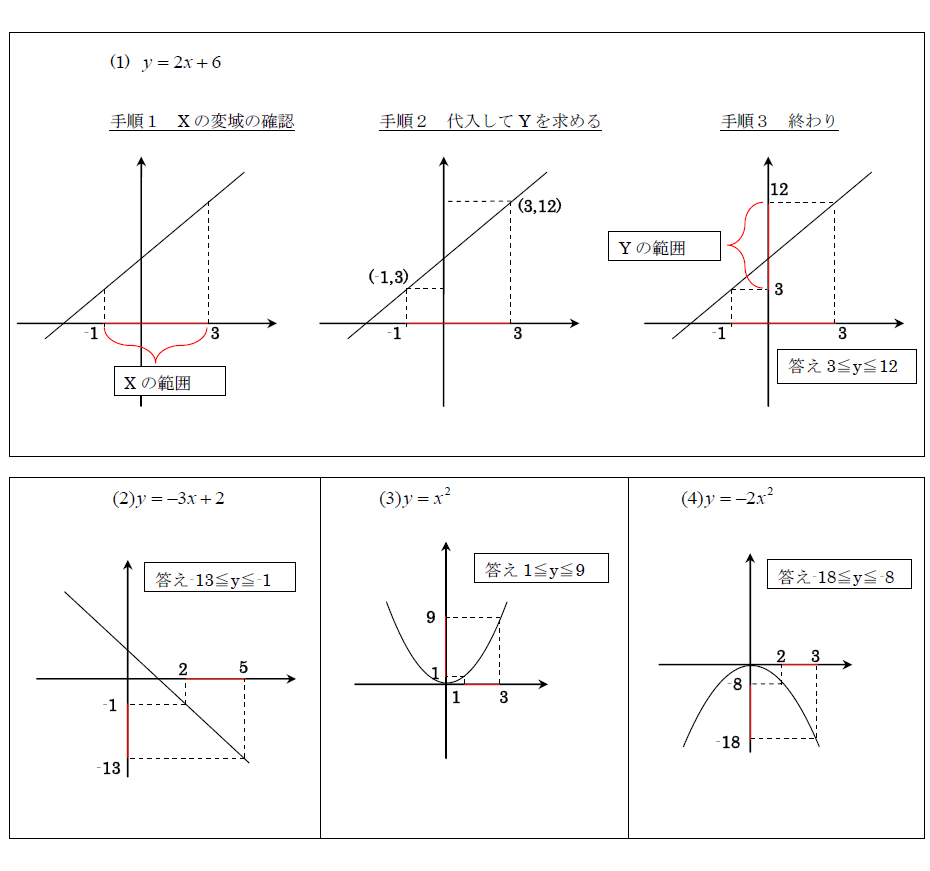



受験 定期試験 数学解き方集 裏技 解法 1次関数 2次関数の変域 中学数学



中3数学 2次関数 原点に頂点がない三角形の面積の求め方




中学数学問題集 中3 2次関数 19 2 中学数学高校数学個別指導in山形市 数専ゼミ
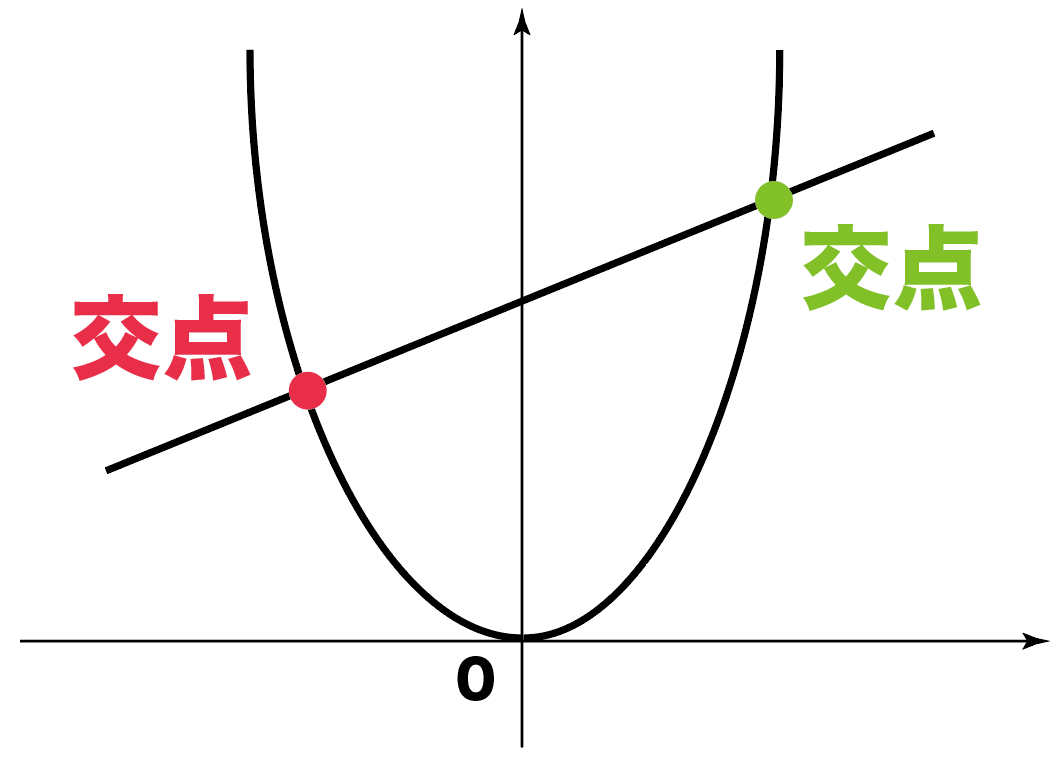



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
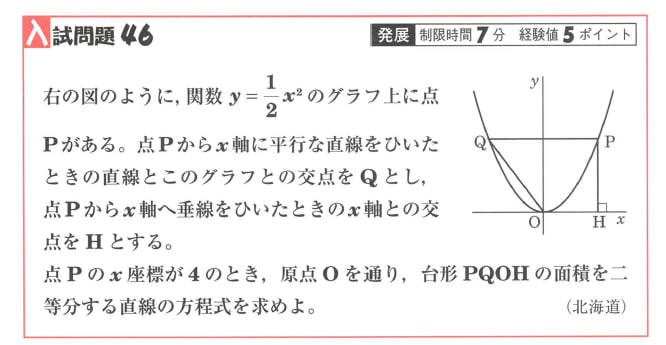



中学数学 1次関数 2次関数 46 北海道 宮城県 高校入試問題 英語 数学 さくら教育研究所 中学 高校受験 Skredu
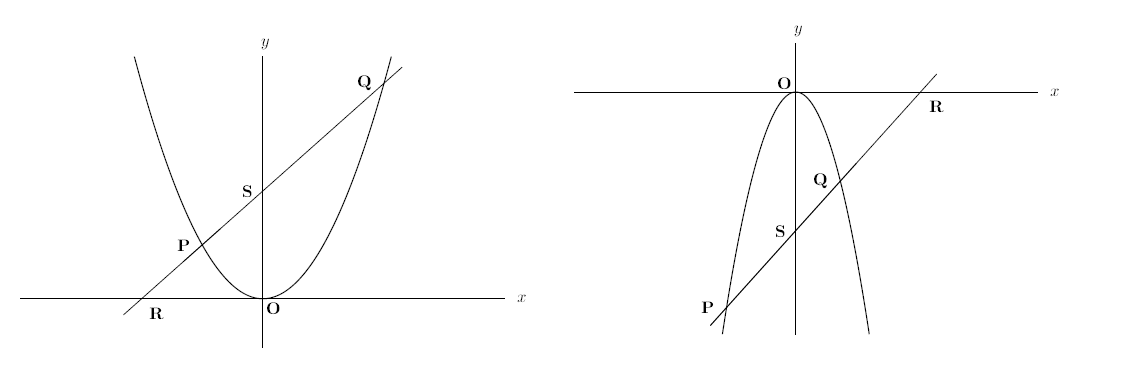



かみのドリル 2次関数と直線に関する問題のドリル 中学



中3数学 二次関数15 関数y Ax 2の利用 図形の移動 すべて無料 星組の中学数学講座



1



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su
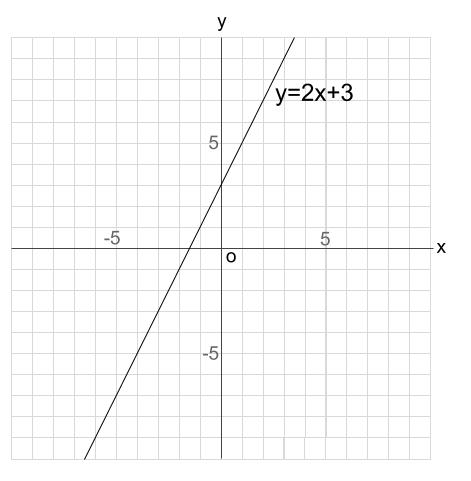



中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su
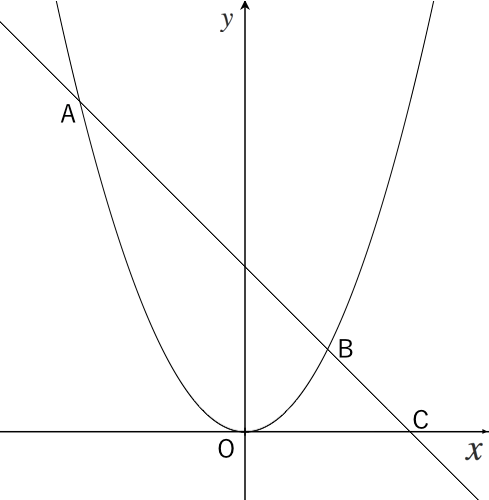



二次関数の利用 グラフ系の問題 苦手な数学を簡単に




中3 数学 4 10 二次関数の利用 面積 Youtube




2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張




ねこ騙し数学




数学 中3 33 二次関数って Youtube
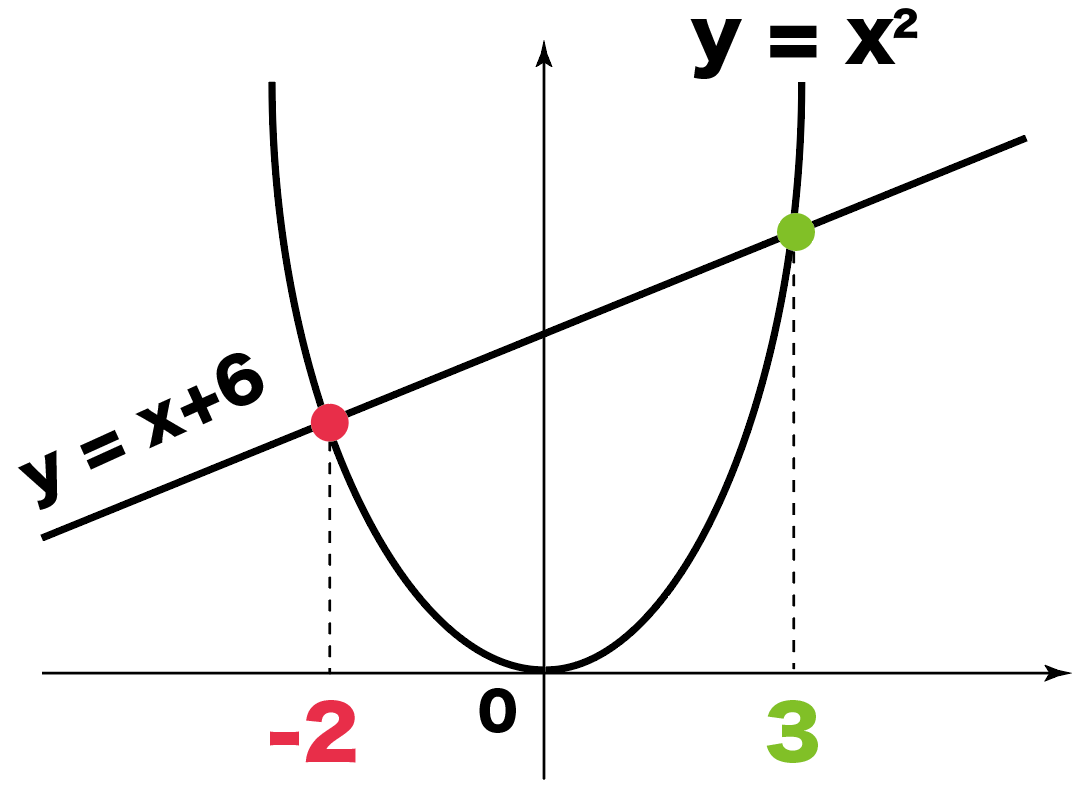



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




二次関数 グラフ 問題 中学 シモネタ



中学数学 Y Ax 2 と変域 中学数学の無料オンライン学習サイトchu Su
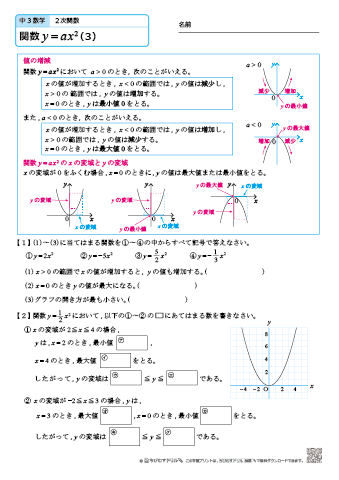



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Formula34 2次関数上の三角形の面積 難関高校合格のための中学数学公式一覧 10秒で解けますか




中学生の数学 1 2次関数の変域の問題での考え方と実例 塾講師が数学をやりmath




二次関数 中学三年生 クラス授業 海星学院 泉校 京都府八幡市男山泉3 21




数学苦手な高校生向け 二次関数グラフの書き方を初めから解説 数スタ




変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学




2次関数 膨大なページ数 Wiki




2次関数 中学3年生 2次関数 数学 Youtube




二次関数のグラフと問題の解き方 覚えておくべき2つの公式
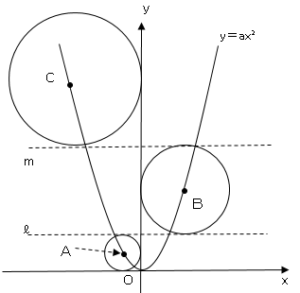



円と関数の関係 数学の要点まとめ 練習問題一覧




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月




1次関数と2次関数があわさったグラフの問題 中学数学 By はっちゃん マナペディア




これで点が取れる 単元末テスト 中3数学 4章 二次関数



中学数学二次関数の応用問題です 学校での練習問題なのですが Yahoo 知恵袋
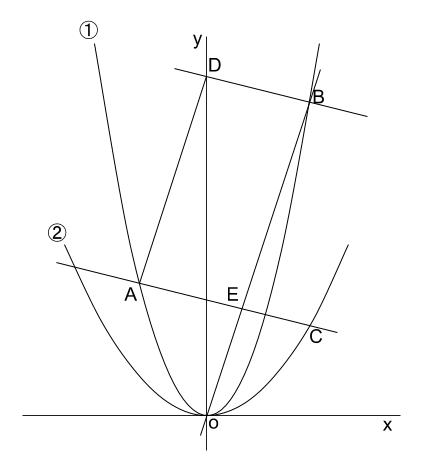



2乗に比例 平行四辺形の難問 中学数学の無料オンライン学習サイトchu Su




なんで中学教科書では 関数y Ax2 を二次関数と呼ばないの Qikeru 学びを楽しくわかりやすく



1
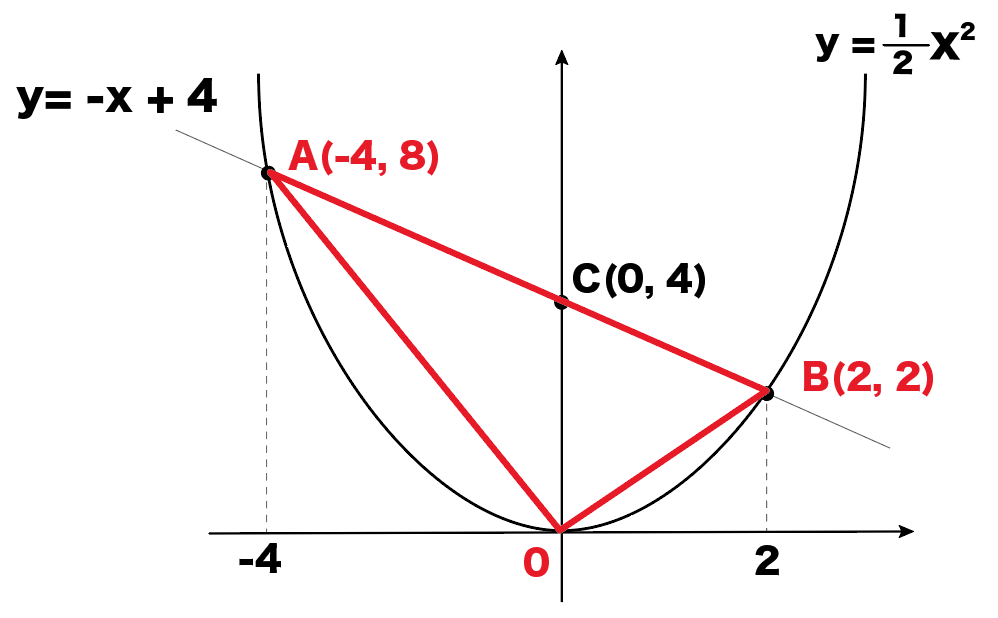



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
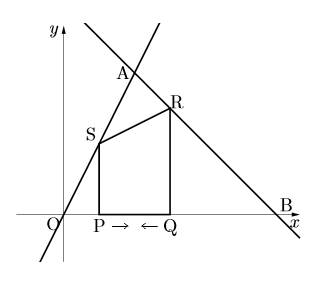



中学数学 二次方程式の応用問題 市川高校 一次関数 数樂管理人のブログ



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師




世界一わかりやすい数学問題集中3 4章 二次関数
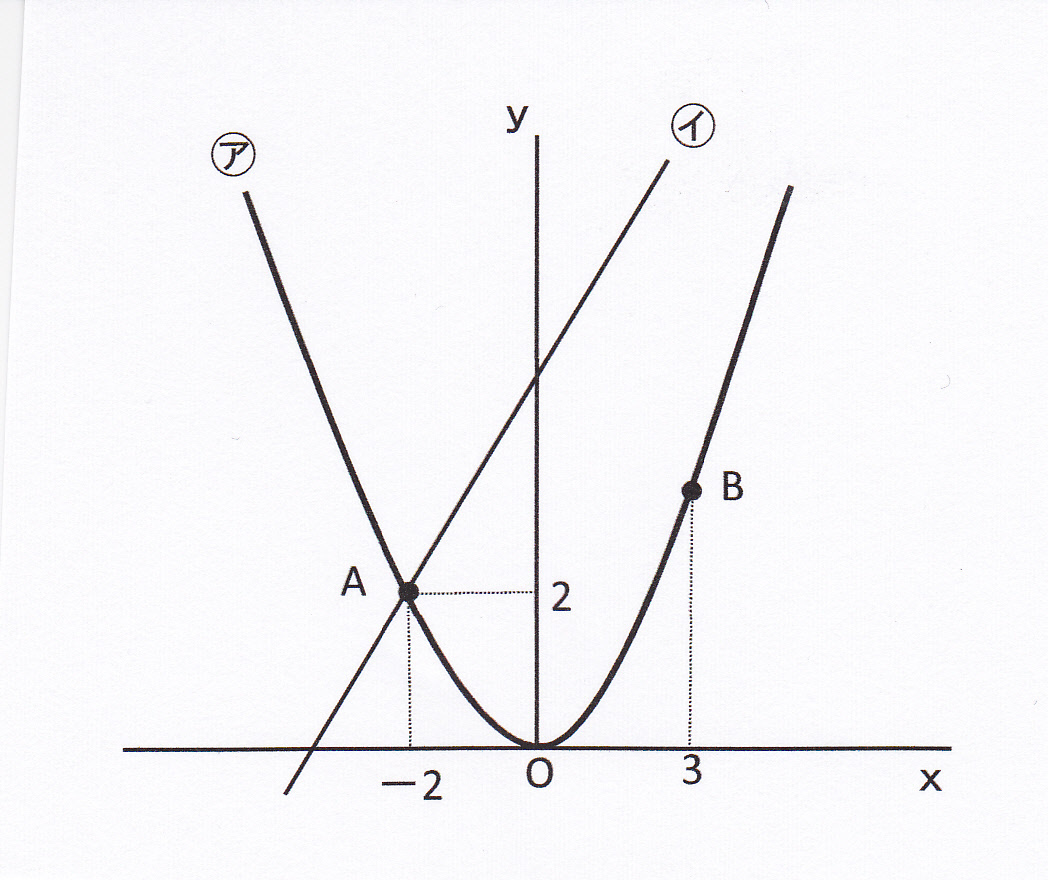



二次関数と一次関数の融合問題の解き方 座標 変化の割合 など 現役塾講師のわかりやすい中学数学の解き方
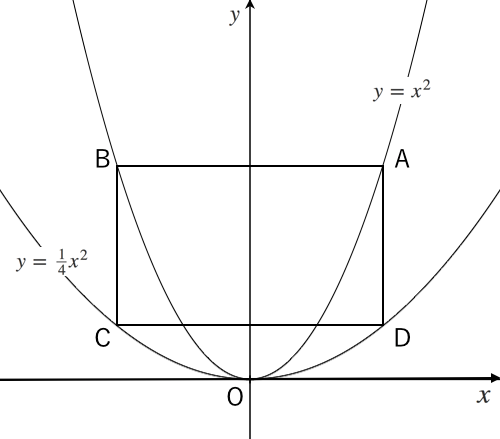



二次関数の利用 長方形 苦手な数学を簡単に



数学 中3 37 二次関数の変域 Youtube




中学3年数学 二次関数 二次関数では必須の平方完成 やり方と成り立ちをわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト




数学 中3 41 二次関数の利用 一次関数とのコラボ編 Youtube




バカでもわかる 中学数学 2次関数




中3 中3 数学 二次関数 中学生 数学のノート Clear




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく



中3数学 2次関数と等積変形の利用のポイント



中学数学単元別 2次関数 数学 中学校 教材 問題集 304 学林舎 通販 Yahoo ショッピング




中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年数学 二次関数の問題です 大問3 4 6 8を解説付きで教えてください Clear




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




2次関数とその応用 英語 数学 さくら教育研究所 中学 高校受験 Skredu




1分でわかる 中学数学 2次関数の最大 最小問題をわかりやすく解説 Youtube
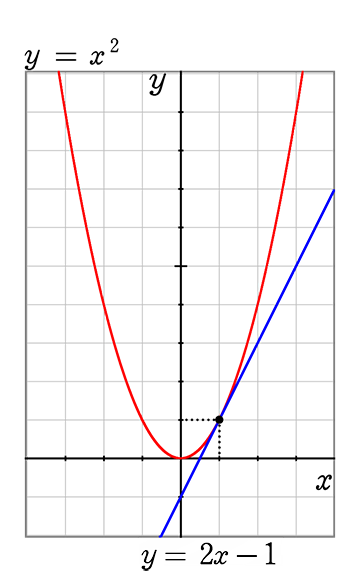



中学数学 関数



二次関数のグラフの書き方と 頂点 軸 切片の求め方 受験辞典




数学 中3 35 二次関数のグラフ Youtube



2次関数のグラフと直線



3次関数はどうなる 中学から数学だいすき




一次関数のグラフ 無料で使える中学学習プリント



中学の数学の範囲で 二次関数と円の交点の座標を求めることは可能 Yahoo 知恵袋




数学 中3 40 二次関数の利用 動点編 Youtube




中学数学問題集 中3 2次関数 19 1 中学数学高校数学個別指導in山形市 数専ゼミ




中学3年数学 二次関数 平方完成を使って二次方程式を解く 数学の面白いこと 役に立つことをまとめたサイト
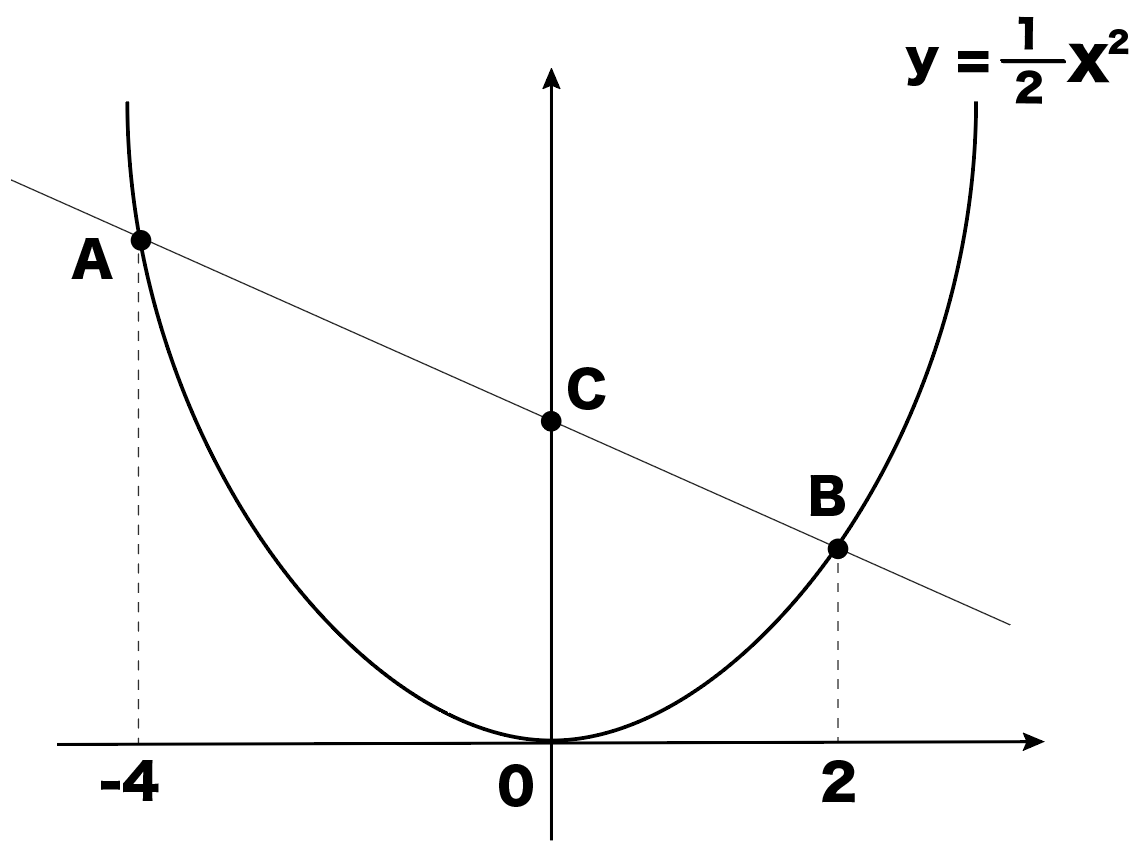



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく



中学数学単元別 2次関数 数学 中学校 教材 問題集 304 学林舎 通販 Yahoo ショッピング



1
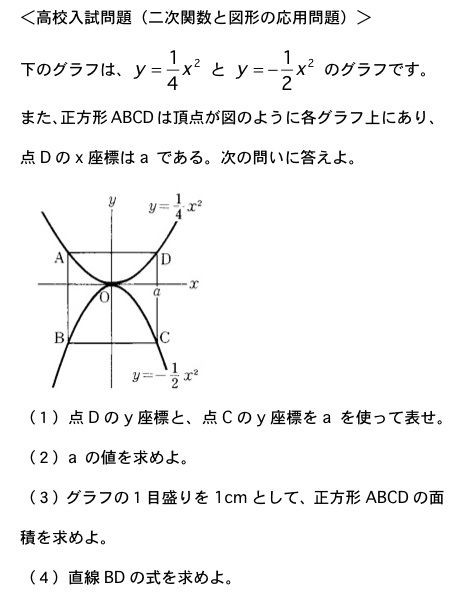



中学3年生2学期の数学の中間テスト 期末テスト問題 2次方程式 2次関数 素敵な話題



0 件のコメント:
コメントを投稿