11年度数学I演習第11回 理II・III 17, 18, 19組 12 月15 日清野和彦 問題1 f を(0,0) 以外で定義された2 変数関数 f(x,y) = x2 −y2 (x2 y2)2とする。また、1より小さい二つの正実数a, b に対し有界閉集合Da,b を0,1×0,1 から0,a)×0,b) を取り除いたものとし、{a n}∞ =1と{bn}∞ を単調に減少して0 にワードで2乗を入力する場合、「2」を選択して「右クリック⇒フォント⇒文字飾りの上付き」にチェックを入れましょう。 またワードの「ホーム⇒フォント」にxの2乗を意味するボタンがあります。 2を選択して、このボタンをクリックすれば2乗に変換されます。 今回はワードで2乗を入力する方法、上付き文字の表し方、数式の使い方について説明します。 2乗の1/5 オープニング(1分55秒) 2/5 円 x 2 +y 2 +lx+my+n=0(5分38秒) 3/5 平方(かっこの2乗)の形の作り方(5分17秒)

Y 3分の1x2乗 2xのグラフの x切片の求め方を教えて下さい Y 0のときの途中 Clear
Y=x2乗分の1
Y=x2乗分の1-2変数x,yについての多項式で、2次の項ばかりからなるもの すなわち、 Q (x,y) = ax 2 2 bxy c y 2 (a,b,cは定数) のことをいう。 ※詳細→2変数2次形式 文献 ・高橋『微分と積分2』§31定理36 (p67) 定理:2次同次関数の標準形 文献微積分学II 演習問題 第9 回 長方形の領域での重積分 40 微積分学II 演習問題 第10 回 縦線図形における重積分 42 微積分学II 演習問題 第11 回 重積分の変数変換 47 ex2y2 1 x 2y (14) lim (x y)!(0 0) sinxy (15) lim (x y)!(0 0) 1 cos




中学数学 文字を用いた四則計算
Y の f による逆像 f-1 ( y) は、「1個の 実数 」からなる。 つまり、「 R = ( -∞,∞ ) で定義された1変数関数 y=f (x)= x3 」は 単射 。 したがって、「 R = ( -∞,∞ ) で定義された1変数関数 y=f (x)= x3 」には、 逆関数が存在する 。 ・「 実数 y の『 RX 2 の微分は 2x だから 3x 2 の微分は 6x これらを引くと y' = 30x 5 −6x ※ 数IIでは,「定数との積」を除いて関数の積の微分公式がありません。 そこで,関数の積は,まず展開してから微分します。 (3) y = (x1)(x2) 考え方 y = x 2 3x2 だから y' = 2x3 (4) y = (2x1) 2A x の微分法 a x をxで微分するとどうなるか考えてみよう。 まずは、底の変換をして、微分することをやってみよう。 いいかな。結果は覚えておこう。 つぎに、両辺の対数をとる方法。
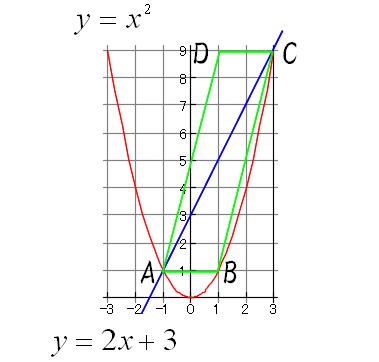
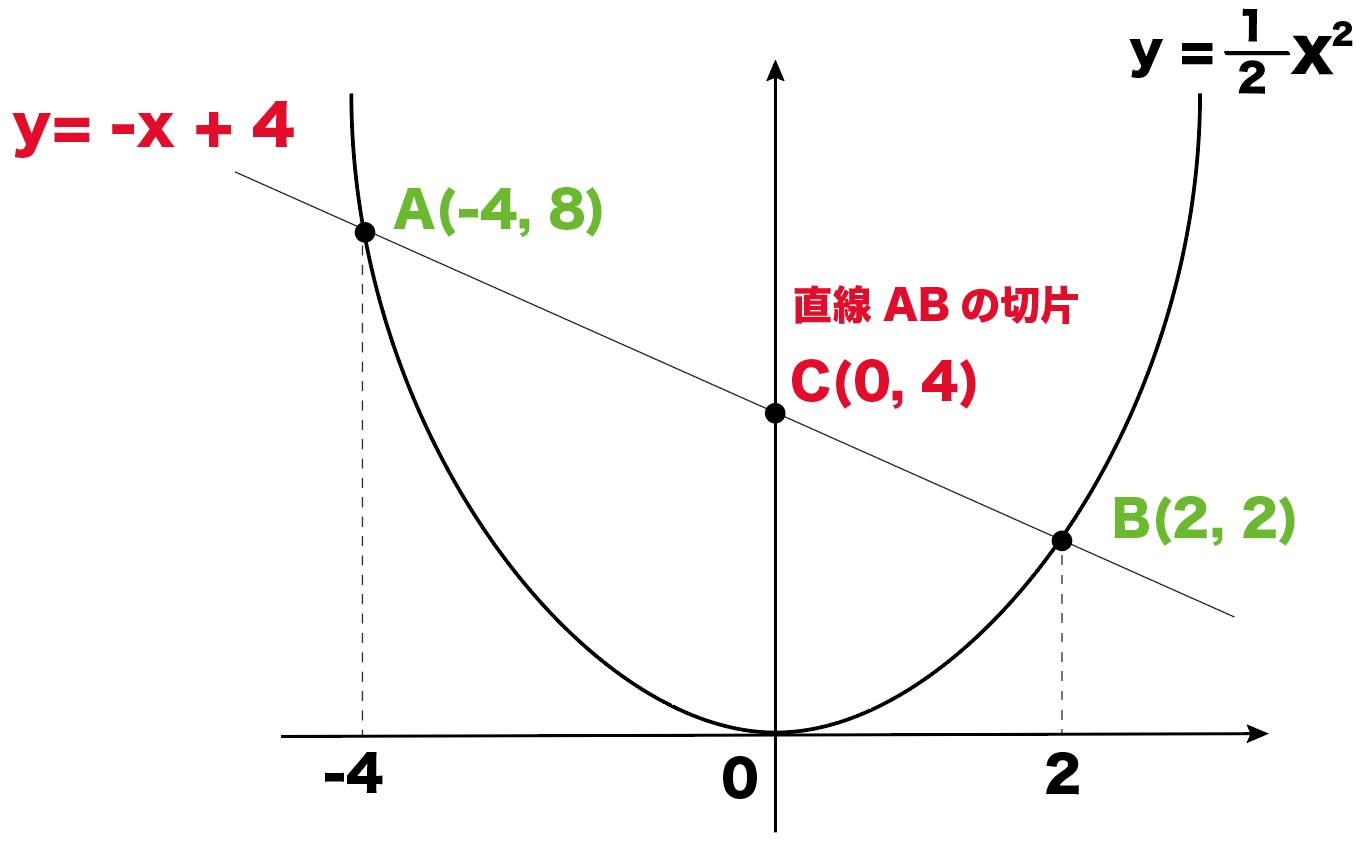
カイ2乗分布(グラフ) 12 /2件 表示件数 5 10 30 50 100 0 1 1547 男 / 40歳代 / 教師・研究員 / 役に立った / 使用目的 自由度の大きさに応じてカイ自乗分布の形がどのように変化していくかを初学者に示す際に役立った 2 1627 女 / 50歳代V = y x2 に対するJacobian @(x;y) @(u;v) を求めよ. (2)重積分 ZZ D (x6 y6)dxdy;解説 この平行四辺形の面積を、「底辺×高さ」から求めようとするのは 無謀ですね。 下のように、よく知った三角形 2 2 つに分けるのが楽なパターンです。 AB A B を通る直線の式が y = −x6 y = − x 6 と簡単に求まるので、 この直線の y y 切片は 6 6 です
べき乗・累乗 1の365乗は1ですが、101の365乗は3778にもなります。 毎日の少しの努力を忘れないために。 流行りつつあるclubhouse。 招待性は特別感があるけど、1日に2人増えると、30日で10億人になる。 32の01乗でいいんだよね? ^^; 大学の物理課題に式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味,関数 y = ax2 y = a x 2 のグラフの特徴,直線の式の求め方を理解する 発展的な三角関数の積分公式 ここから先は公式を丸覚えするというよりも導出方法をしっかり理解することが大事です。 ∫ 1 sin x d x = 1 2 log ( 1 − cos x 1 cos x) C \displaystyle\int \dfrac {1} {\sin x}dx=\dfrac {1} {2}\log (\dfrac {1\cos x} {1




積分の面積公式と証明 6分の1公式 接線など 理系ラボ




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks
もう少し簡単な式から考えてみましょう。 (x1)2乗 = x2乗2x1 はわかりますよね? (xa)2乗 = x2乗2axa2乗 も大丈夫かな? 下の式で、右辺のa2乗を左辺に移動しましょう。 どうなりますか? これと今回の問題を比べて見てください。 こういう変形に慣れると、問題を解く力がワンランク上がります。 3 x 2 − 7 x 2 のように「共通する因数でくくっても、 x 2 の係数が 1 にならない式」を因数分解する場合には、「たすきがけ」というテクニックを使います。 文字だけだとピンと来にくいと思うので、具体例を通じてやり方を見ていきましょう。 問③. 3 x1 y = − x2 2 C (6) y = x2 4 1!2 (7) y = Cx1 (8) y2 = C(2x− 1) (9) y =2x (10) y = e−cosx 例題12-2 dy dx = y xを解きなさい (例題12-2の解答) dy dx = yの解y = Cexp(x)を用いて,y = C(x)exp(x) とおいて, C(x)に関する微分方程式をつくる




2 の問題です Xの4乗 4を因数分解するという問題なのですが 2行 高校 教えて Goo




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ
V = y x2 に対して, @(u;v) @(x;y) = det u x u y v x v y! x^2 の積分が (1/3) x^3 になるとは、 正方形を重ね合わせて作った立体の体積が、一辺 x の立方体の 1/3 になる、ということだ。 つまりこれは、四角錐の体積のことだ。 1つ次元を下げて、 x の積分が (1/2) x^2 になるとは、D = (x;y) j1 5 xy 5 2;



1




高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト
平方根・立方根・3分の2乗の説明 諫早湾の目次 本文に戻る グラフはいずれも,x を横軸,y を縦軸にとってあります.また,負(マイナス)の数は面倒になるので考えないことにします. 2乗と平方根X2 5 y 5 2x2 を求めよ. 解 (1) u = xy; 先生 「2の0乗の答えは0じゃなくて1になるんだよ!どんな数も0乗すると1になるんだ。凄く大切だから覚えておいてね☆」 あなたも先生にこんな教わり方をしませんでしたか? けど「0乗すると、なんで1になるの?」って理由を聞




高校数学 2次関数がx軸から切り取る線分の長さ 受験の月



1
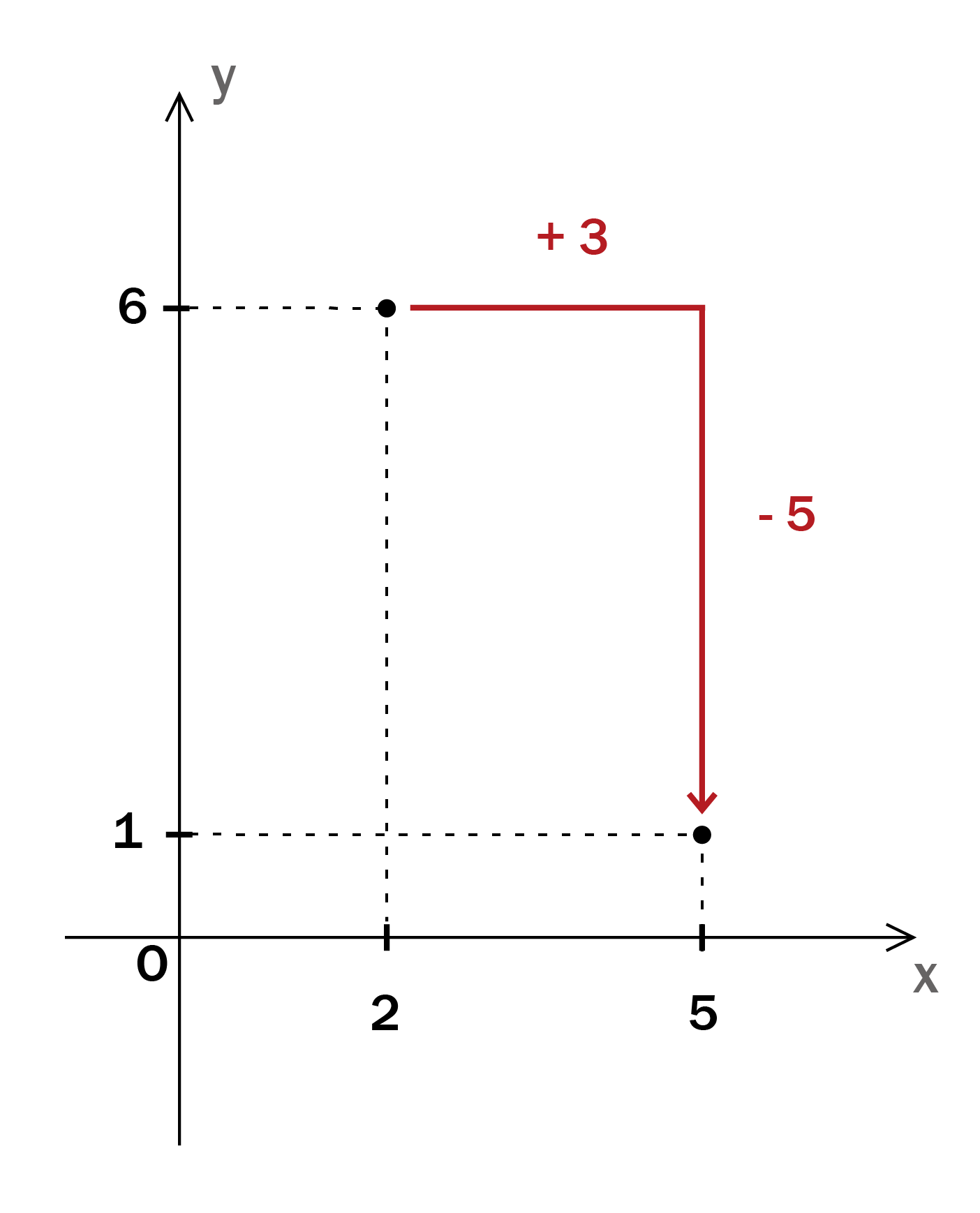
よって,求める曲線の方程式は,Y=2(X2) 2 1 となります。 ゆえに,平行移動した後の曲線の方程式は,y=2(x2) 2 1,すなわち,頂点 (2,1),軸 x=2 の放物線となります。 放物線 y=2(x2) 2 1 をよく見て見ますと,この式の中に頂点 (2,1) の座標が表れています。 上の結果を,実際,右のグラフを次の重積分を計算せよ. ∫ 0 2 ∫ y 2 1 (x y) d x d y 解答 ∫ 0 1 ∫ 0 1 − x (x 2 − 2 y) d y d x 解答= det y x 2y x 2 1 x!



Xの二乗分の1 yの2乗分の一を通分するとなぜxの2乗yの2乗分のxの二乗 Yahoo 知恵袋




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ
なぜ2分の1乗がルートなのか 例えば、$(5^2)^3=5^6$ というように、$5$ という数を $2$ 乗 してから $3$ 乗 したものは、 $2\times 3=6$ 乗 したものと同じです。 これと似たような法則 「 $\dfrac{1}{2}$ 乗 してから $2$ 乗 したものは、 $1$ 乗 したもの」 1.2重積分とは まずは2重積分とはどんなものかを説明していきましょう。 今まで習った1変数の関数の積分のイメージは 積分区間を細かく刻み、細かく刻んだ部分の長方形の面積をすべて足したもの でしたね。 では、2変数関数、つまり2重積分の場合だとどうなるでしょうか。二乗に比例(ひれい)とはy=ax 2 のように「yの値がxの2乗に比例する」ことを言います。 また、単に比例というとy=axのような式のことです。なお「y=ax 2 b」は比例関係では無いので注意しましょう。 比例とは、ある値が2倍、3倍と増える時、もう一方の値も同様の比率で増える関係をいいます。



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf
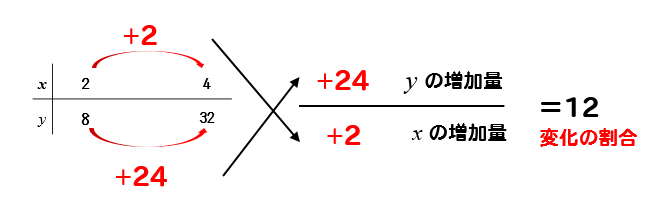



変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ
(類題12-1の解答) (1) y = −log(C −ex) (2) y = Ce12x 2 (3) x2 y2 = C (4) y = log(ex C) (5) y =0;5分でわかる! 「yはxの2乗に比例」とは? 映像授業 Try IT(トライイット) 541K subscribers Subscribe 中3 数学 関数y=ax^2② x^2に比例 (9分) Info Shopping よって、 ∫x^ (a1)dx= (1/a)*x^a+C →∫x^adx= {1/ (a1)}*x^ (a1)+C となります。 つまり、 ∫1/x^2 dx=∫x^ (2)dx = {1/ (21)}*x^ (21)+C =-x^ (1)+C =-1/x+C
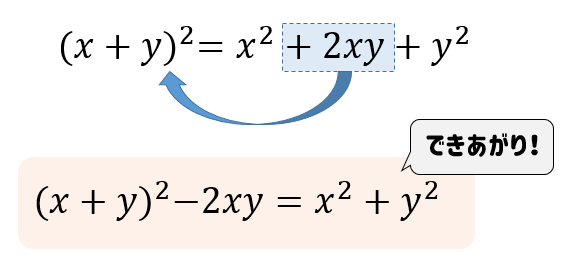



二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ
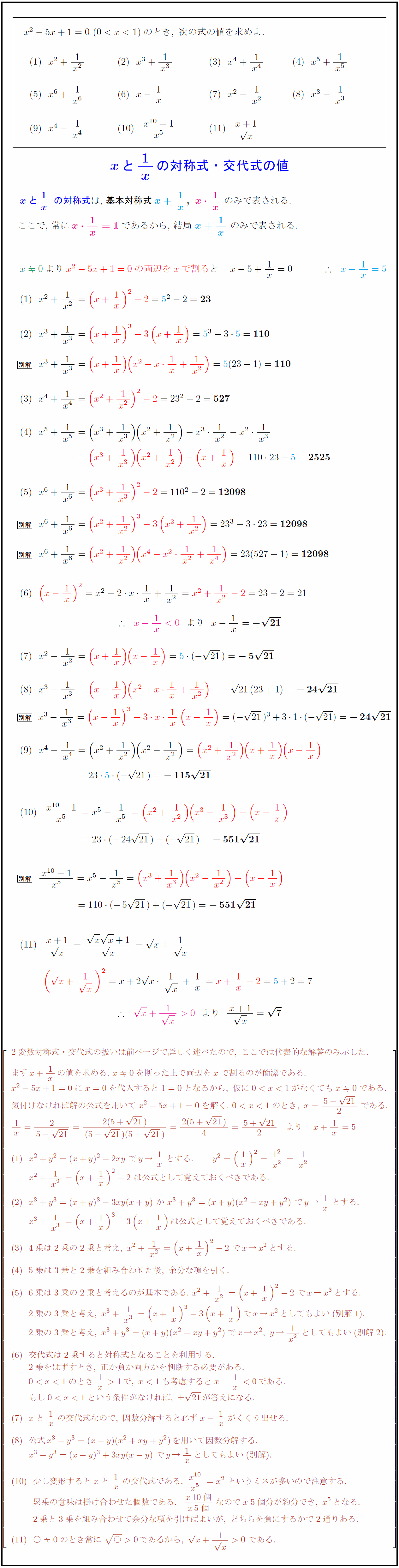



高校数学 Xと1 Xの対称式 交代式の値 X 1 X X 1 X X 1 X など 受験の月
公式1: ∫ d x x 2 a 2 = log (x x 2 a 2) \displaystyle\int \dfrac{dx}{\sqrt{x^2a^2}}=\log(x\sqrt{x^2a^2}) ∫ x 2 a 2 d x = lo g (x x 2 a 2 ) 公式2: ∫ x 2 a 2 d x = 1 2 ( x x 2 a 2 a 2 log ( x x 2 a 2 ) ) \displaystyle\int \sqrt{x^2a^2}dx=\dfrac{1}{2}(x\sqrt{x^2a^2}a^2\log(x\sqrt{x^2a^2})) ∫ x 2 a 2 d x = 2 1 ( x x 2 a 2 a 2 lo g ( x x 2= 3y x2 よって @(x;y) @(u;v) @(u;v) @(x;y) = 1であるから, @(x;y) @(u;v) = @(u;v) @(x;y) 21 = x 3y 3例:y={(1/2)^x}1(2分の1のx乗プラス1) 使い方 式の入力には、数字と「x * / ( ) { }」を使用します。すべて半角です。 ×は「*」、÷は「/」を用います。 絶対値記号やガウス記号を使用することもできます。べき乗は、{底^指数}で表現します。 例:y=x, y=x, y={2^x}




中3数学 Y 2分の1x2乗のグラフと変域 5分で学習 Youtube



2次関数の問題で Y X2乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋
数学 中学生 1年以上前 あんころもち y=1/2x^2 (二分の一エックスの二乗)のグラフを書いてみたのですが、これでいいのでしょうか グラフに点を取るときに、偶数を当てはめたんですが (a=1/2のため)、そうすると点は2と4 (2と4)しかとれません xが4以上例1 y=x 2 2x の増減表を求めるには: 微分して y ' を求める y '=2x 2=2(x 1) となる y '=0 となる x の値を求める y '=0 となる x の値は 2(x 1)=0 より x=1 y ' の符号を求める x基本的な関数の微分 1 x 2 問題 次の関数の導関数を微分の公式および導関数の定義式を用いて求めよ. f (x) = 1 x 2 答 f ′ (x) = − 2 x 3 解説 f (x) = 1 x 2 = x − 2 と表すことができる. 公式を用いた計算 微分の公式を用いると, f ′ (x) = − 2 x − 2 − 1 = − 2 x − 3 = − 2 x 3 となる.




中3数学 Y X2乗のグラフ 5分で学習 Youtube




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ
つまり, を2乗すると3になりますね。 では, を2乗してみると,どうなるでしょうか? ここで,①,②より, と言えます。 この両辺の( )の中を比較して, となります。 一般に, と定義します。 例えば, , です。 さらに,指数が, ではなく, の場合はどうなるかを考えましょう。 は,本当は, の2を省略して書いたものなのです。 つまり,3の 乗が と(例3) x 2 6x1=0 x 2 6x1 = 0 ←定数項を右辺に移項する x 2 6x = 1 ←左辺でxの2乗の式を作るため両辺に9を足す x 2 6x 9 = 1 9 ←左辺を因数分解すると(x3) 2 になる (x3) 2 = 10 ←平方根 x3 = ± 10 ←3を移項 x = 3± 10 不定積分∫(1/x^21)dx の計算について 初投稿です。 現在高校2年生です。 先取りで数ⅢCの内容を勉強しています。




Y x二乗 xの微分を教えてください Peing 質問箱



二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い
(1) \ y = x \log x \ (2) \ y = x^3 \sin x \ (3) \ y = \sin x \cos x \ 5.練習問題の答え 解答1 何回か微分して \( n \) 次導関数の項を予測する。 (1) \( y = (1x)^{1} \) とすると計算がしやすく




Eの2x乗の微分や積分は Eの3x乗の微分や積分は Eのマイナスx乗の微分や積分は E 2x E 3x E X ウルトラフリーダム




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書




数学小話 いろいろ拡張しよう マイナス2分の1乗とは 日比谷高校のススメ



2 裏業



X2乗 1分の3x 5 X2乗 X分の1の解き方を教えてください こ Yahoo 知恵袋




この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave




Y 1 X 2乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo




積分の面積公式と証明 6分の1公式 接線など 理系ラボ



Yx2乗 ニスヌーピー 壁紙




Y 3分の1x2乗 2xのグラフの x切片の求め方を教えて下さい Y 0のときの途中 Clear




数学 計算 X二乗 Xy Y二乗 X二乗 Xy Y二乗 X4乗 X二乗y二乗 数学 教えて Goo




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks



X 1分のx2乗 X分の1の解き方を教えてください ただの通分 Yahoo 知恵袋



Yx2乗 ニスヌーピー 壁紙




積分の面積公式と証明 6分の1公式 接線など 理系ラボ
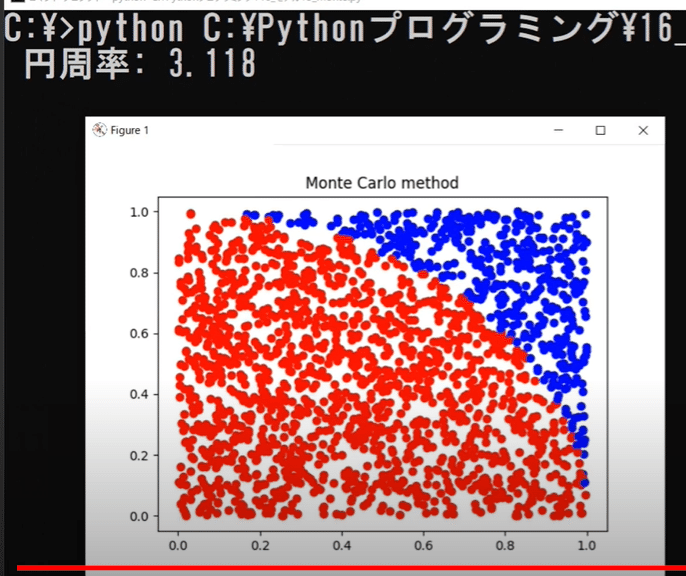



高校情報1 シミュレーション 確定モデル 確率モデル 円周率とモンテカルロ法 Pythonプログラミング 教員研修用教材 学習16 高校情報科 情報処理技術者試験対策の突破口ドットコム Note




中3数学 Yはxの2乗に比例 とは 映像授業のtry It トライイット




19 号 放射線治療計画における分画選択ツール Astamuse




積分の面積公式と証明 6分の1公式 接線など 理系ラボ
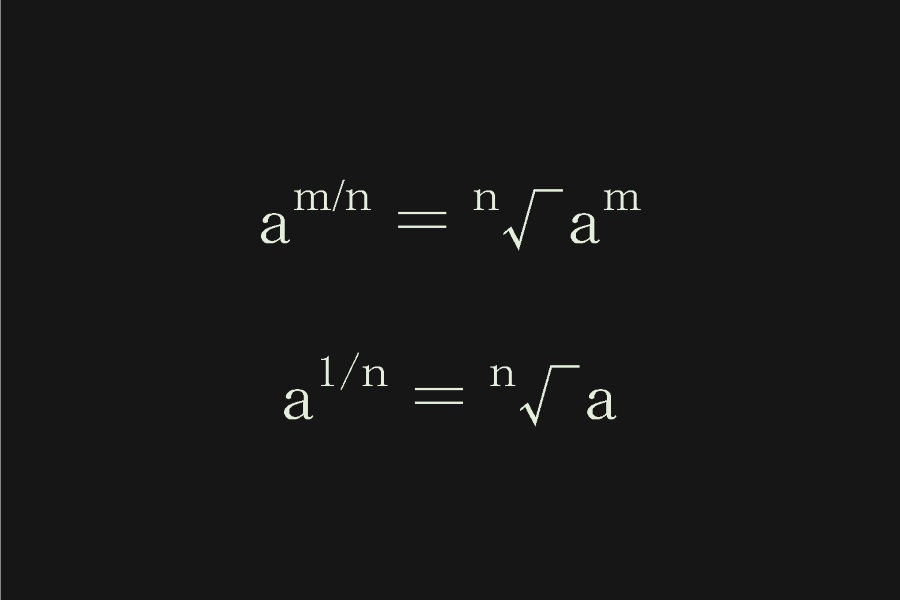



指数法則の一覧 統計学でよく使うもの 統計学が わかった




この2問の解き方を教えてください 答えは 5 が 6 が です Clear




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube




数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo




二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ



Y 2分の1x2乗のグラフ y 4分の1x2乗のグラフの書き方を教えて Yahoo 知恵袋



Yx2乗 1 ニスヌーピー 壁紙



二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い




これがわかりません Clear



0gibi1zgsfiuem
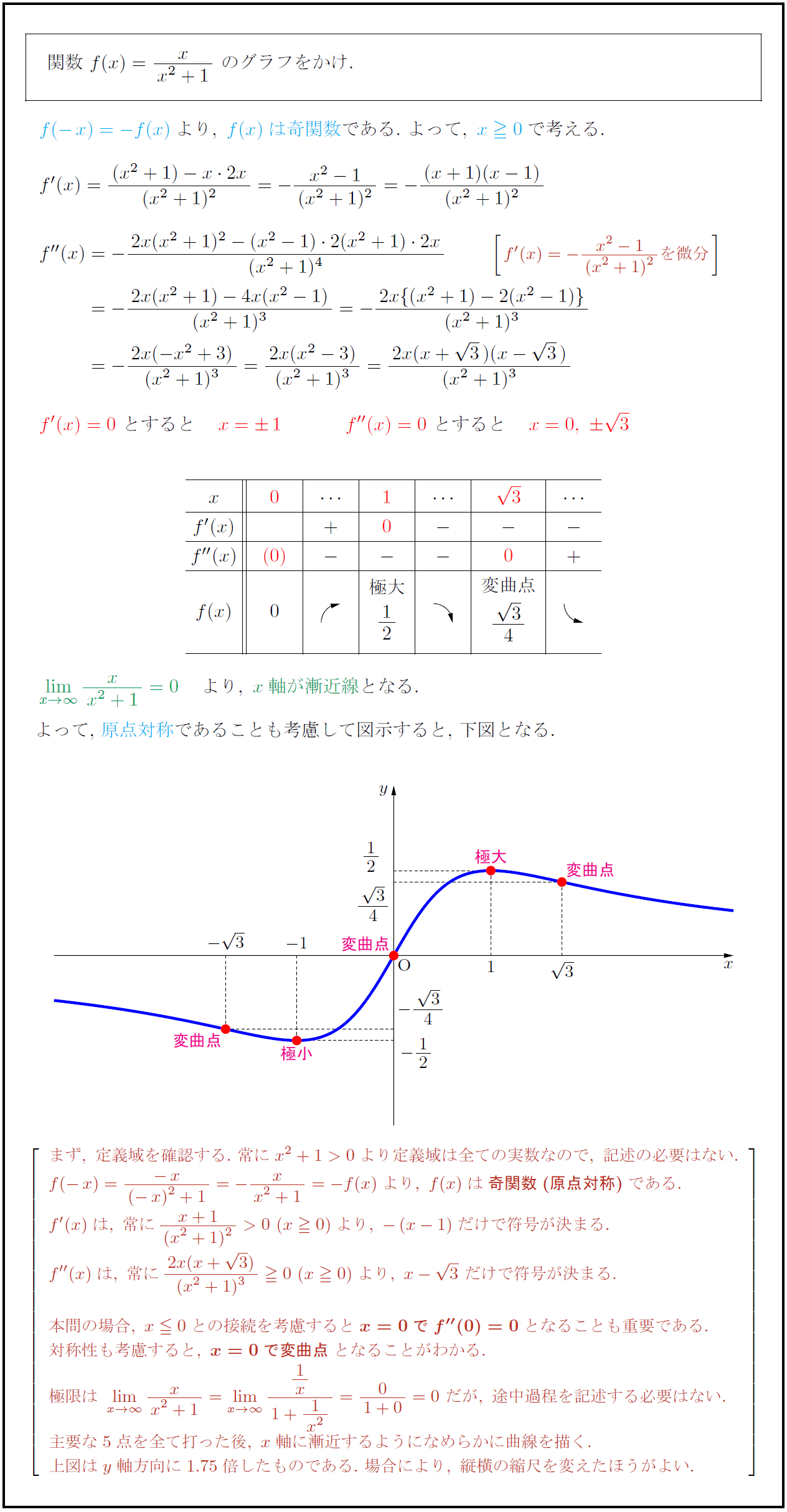



高校数学 分数関数 Y X X 1 のグラフ 受験の月




1 12公式 3次関数 おいしい数学




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット




3分で分かる 絶対値を含む不等式の解き方をわかりやすく 合格サプリ




指数 対数関数 2分の1乗の意味 数学 定期テスト対策サイト




中学数学 文字を用いた四則計算




差分和分 怜悧玲瓏 高校数学を天空から俯瞰する



Y X X2乗 1のグラフ 画像の答えが理解できません なぜ Yahoo 知恵袋



Xの二乗分の1 yの2乗分の一を通分するとなぜxの2乗yの2乗分のxの二乗 Yahoo 知恵袋




因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ




数学です Y 1 X 2のグラフで X 2のときは X 2に近づくと無限大に発散す 数学 教えて Goo




X X分の一 3のとき X二乗 X二乗分の一 X四乗 X四乗分の一を求めよ Clear
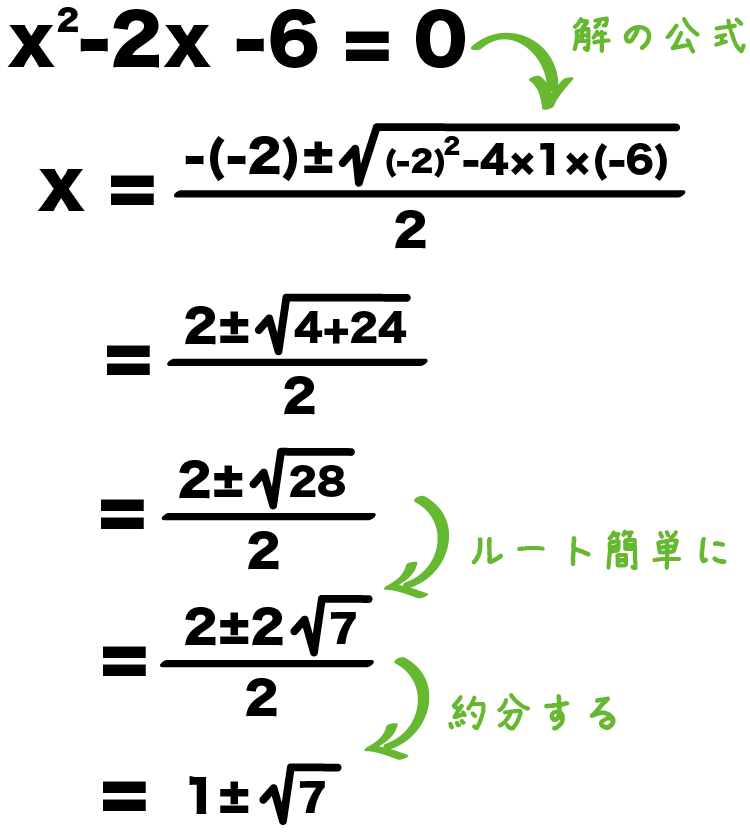



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく




2次関数のグラフ




Y 1 X2乗のグラフ Youtube



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



2 裏業
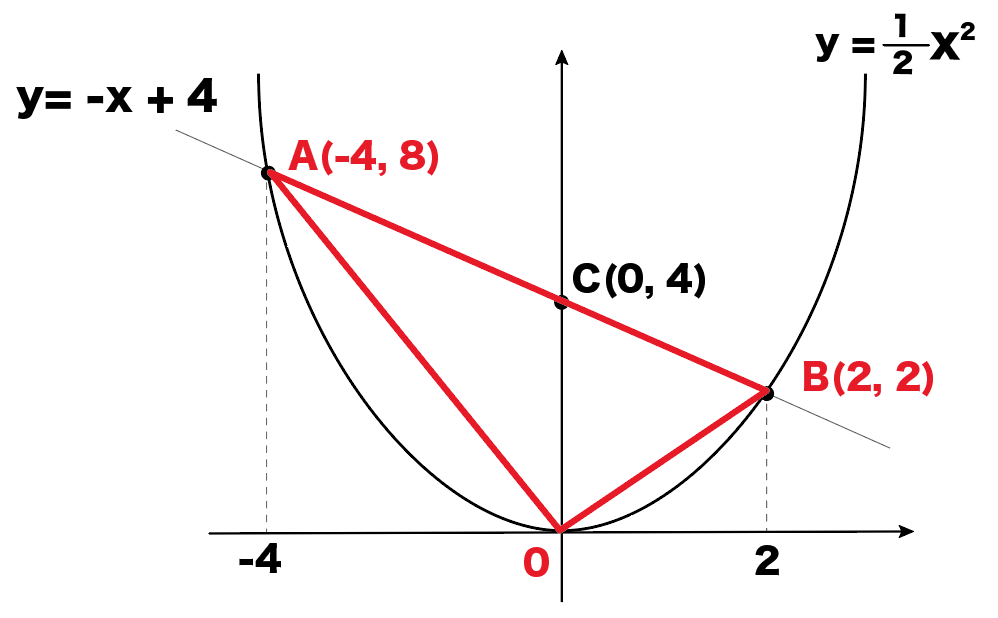



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく



高校数学 特殊な置換をする不定積分 X A を含む不定積分 最高難度 と特殊な置換の根拠 受験の月



Mathematics 2乗に比例 放物線 応用問題の解き方 関数と図形 面積の二等分 等積変形 働きアリ



1



Http Www U Gakugei Ac Jp Onodakk Math Chu32jikansu Jusin2jikan2 Pdf




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




Y x二乗 xの微分を教えてください Peing 質問箱



二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ
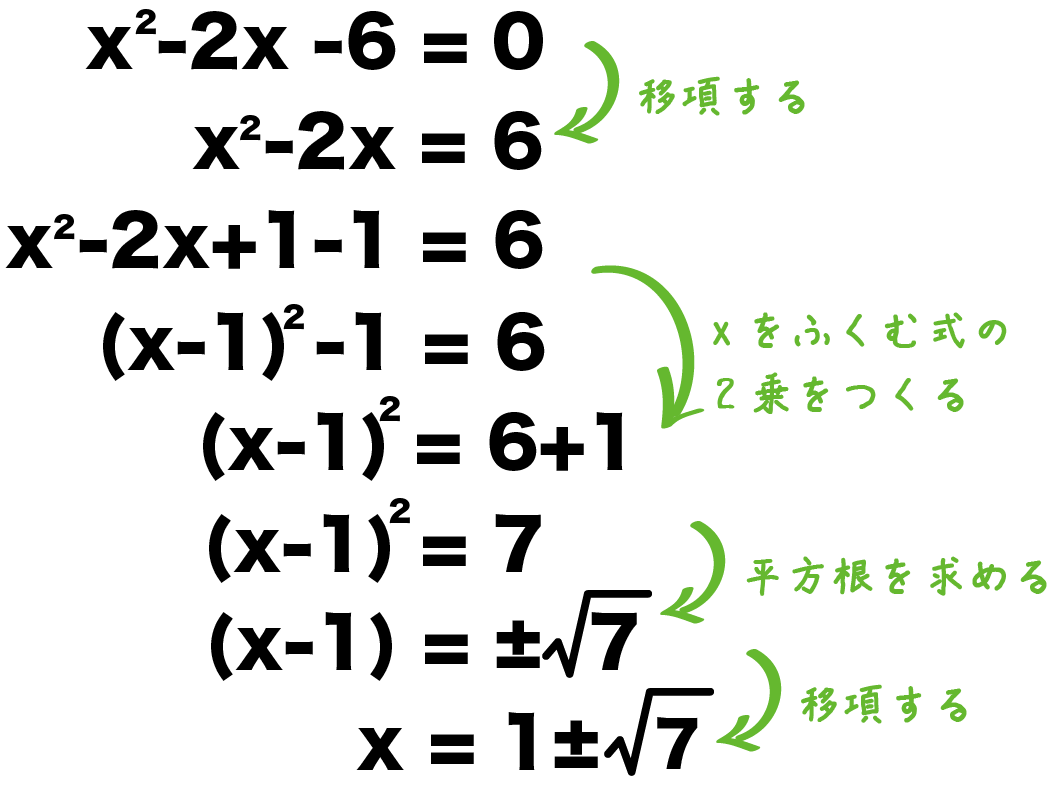



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく



3分の2乗の説明




なぜ4のx乗分の1が2分の1のx乗の2乗になって Clear
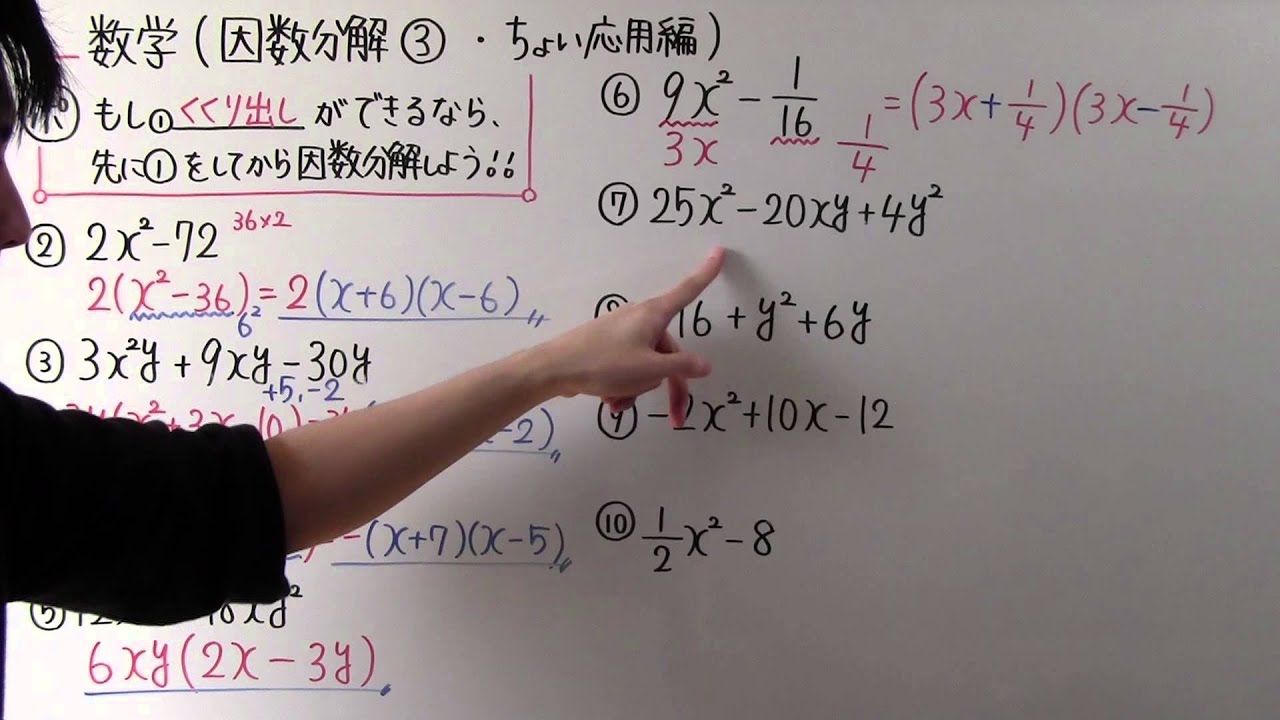



数学 中3 8 因数分解 ちょい応用編 Youtube



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく



Y Xの2乗分のx2乗 1の式を微分してグラフを書く問題があります Yahoo 知恵袋




変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ



Yx2乗 ニスヌーピー 壁紙



Mathematics 関数と証明 大阪府公立 22年前期理数科 働きアリ



Q Tbn And9gcsymbndgo2obahwwjzy0cnswmv6fyuw7arvj7arntyggu15 Naq Usqp Cau



Xの2乗 Xの2乗分の1 7の時t X X分の1とおくとtの2乗 Yahoo 知恵袋



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



3分の2乗の説明




X X分の一 3のとき X二乗 X二乗分の一 X四乗 X四乗分の一を求めよ Clear



Y 1 X2乗のグラフ Youtube
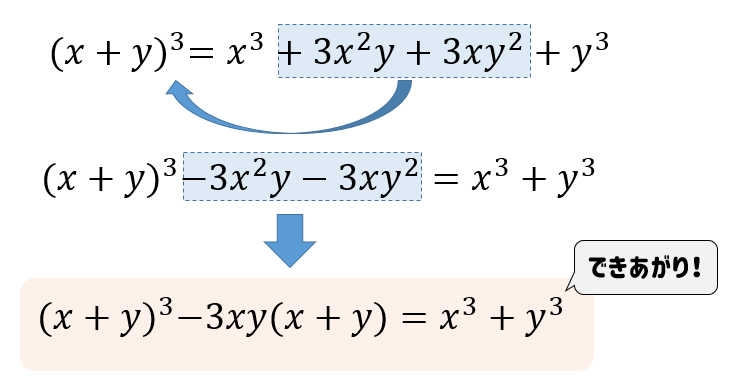



二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ




2 の問題を教えて下さい 何で最後にx2乗を引いてるんですか 2 高校 教えて Goo




これがわかりません Clear




放物線y X 2 0 X 1 の長さ 身勝手な主張



3分の2乗の説明
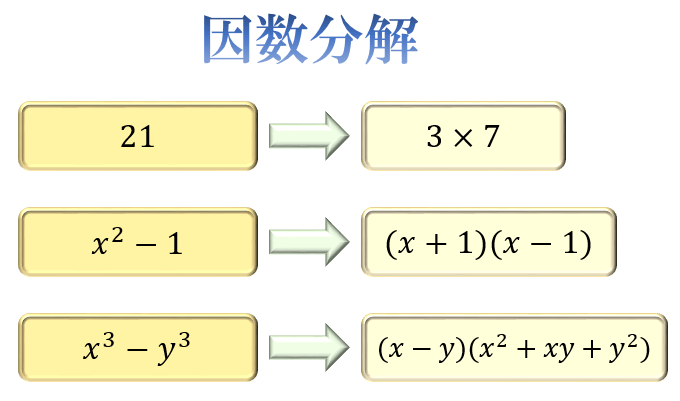



因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ



Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋



2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




積分の面積公式と証明 6分の1公式 接線など 理系ラボ




Yx2乗 ニスヌーピー 壁紙




数学 中3 35 二次関数のグラフ Youtube




偏微分の意味とやり方



0 件のコメント:
コメントを投稿